3 Acquisition des droits
3.1 Imputation de l’âge de décès
3.1.1 Description
L’étape 3.1 permet d’imputer un age de décès pour les populations simulées (générations ≥ 1951). L’imputation des âges de décès des générations observées (générations < 1951, provenant de l’EIR) sont imputées à la suite dans l’étape 3.2.
Les âges de décès sont estimés à partir des coefficients de mortalité différentielle \(\lambda(t)\) (estimés dans le programme 1.25 ). L’âge maximal de mortalité est fixé à 110 (les coefficients de mortalité sont fixés à 100% au delà). Pour rappel, les coefficients de mortalité sont estimés par generation, sexe, quartile de pension de retraite, age.
Une fonction de survie \(S(a)\) est ensuite calculée à partir des coefficients de mortalité instantanée \(\lambda(a)\) calculés à l’étape 1.25 :
\[S(a) = S(a)^{gen, sexe, quartilePension} = \left\{ \begin{array}{cl} 1 & \text{si } a = 2016 \\ \bigcap_{x = 2016}^a 1- \lambda(x) & \text{si } 0<age≤110 \\ 0 & \text{si } age ≥ 111 \end{array}\right.\]
Avec la mortalité instantanée (probabilité de mourir au cours de l’année a sachant qu’on est vivant au début de l’année a)
\[\lambda(a) = \lambda(a)^{gen, sexe, quartilePension} = \mathbb{P}(T=a|T≥a) \]
Et \(T\) la variable aléatoire année du décès.
Un individu est vivant tant que son aléa de décès (aleaMort) est inférieur à la fonction de survie \(S(a)\) (fonction décroissante avec l’année) de sa génération, son sexe et son quartile de sa pension.
A ce stade du modèle, les pensions ne sont pas estimées (cf. programme section 6). La mortalité est cependant estimée lors du programme section 2, afin de supprimer au plus tôt les données portant sur des individus décédés (ce qui permet notamment de diminuer le temps de calcul ainsi que le volume des bases de données). Le quartile de pension est alors approximé par le quartile de rémunération (relatif au SMPT cumulé).
\[ quartilePension_i^{proxy} = quartileRemuCumSmpt_i\]
Avec :
\[remuCumSmpt = \sum_{a = annee1erEmploi}^{anneeMort}\frac{remuneration_a}{SMPT_a}\]
L’âge de mortalité d’un individu est donc déterminé par sa fonction de survie et par un son aléa de décès (tiré lors de l’étape 2.19). Un aléa proche de 0 implique un âge de décès précoce, un aléa proche de 1 implique un âge de décès élevé, tandis qu’un aléa proche de 0,5 implique un âge de mortalité proche de la moyenne.
3.1.2 Résultats
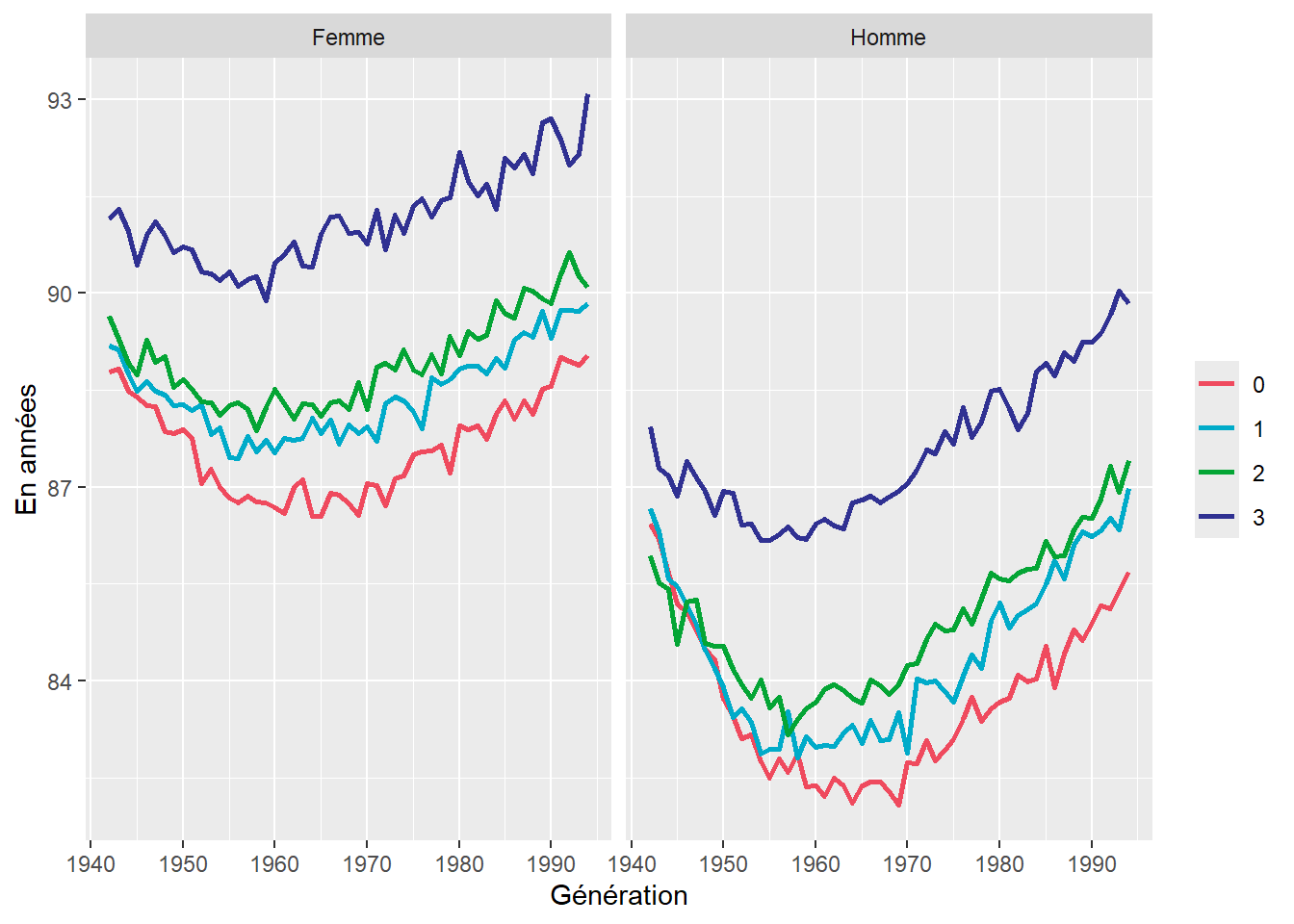
Conformément aux coeffients de mortalité, les femmes vivent en moyenne plus longtemps que les hommes, et l’espérance de vie augmente en fonction du niveau de pension.
3.2 Imputation de l’âge de décès EIR
Réplication de l’étape précédente, mais pour la partie EIR.
3.3 Imputation AVPF
Pour les années où un état AVPF (principal ou secondaire) a été déterminé à l’étape 2.23, on veut désormais imputer un salaire porté au compte au titre de l’AVPF (appelé montantAvpf). Pour cela, on utilise la distribution calculée à l’étape 2.15 ainsi que l’aléa de trimestres gratuits de chaque individu.
Dans le détail, un nombre de mois passé à l’AVPF (ou nombre de Smic AVPF) est imputé. Puis, on multiplie cette quantité par la valeur du Smic AVPF (=169 heures Smic ; assiette forfaitaire sur laquelle les cotisations sont calculées) afin d’obtenir le montant AVPF qui sera additionné à la rémunération dans le calcul du SAM à l’étape 6.6.
Le montant de l’AVPF pour une année donnée \(a\) est donc calculé comme suit :
\[montantAVPF_a = nbSmicAvpf_a \times SmicAvpf_a\] De leur côté, les trimestres acquis au titre de l’AVPF sont déterminés à l’étape 3.4.
Pour information, le montant AVPF moyen versé varie beaucoup selon l’âge, comme l’illustre le graphique ci-dessous.
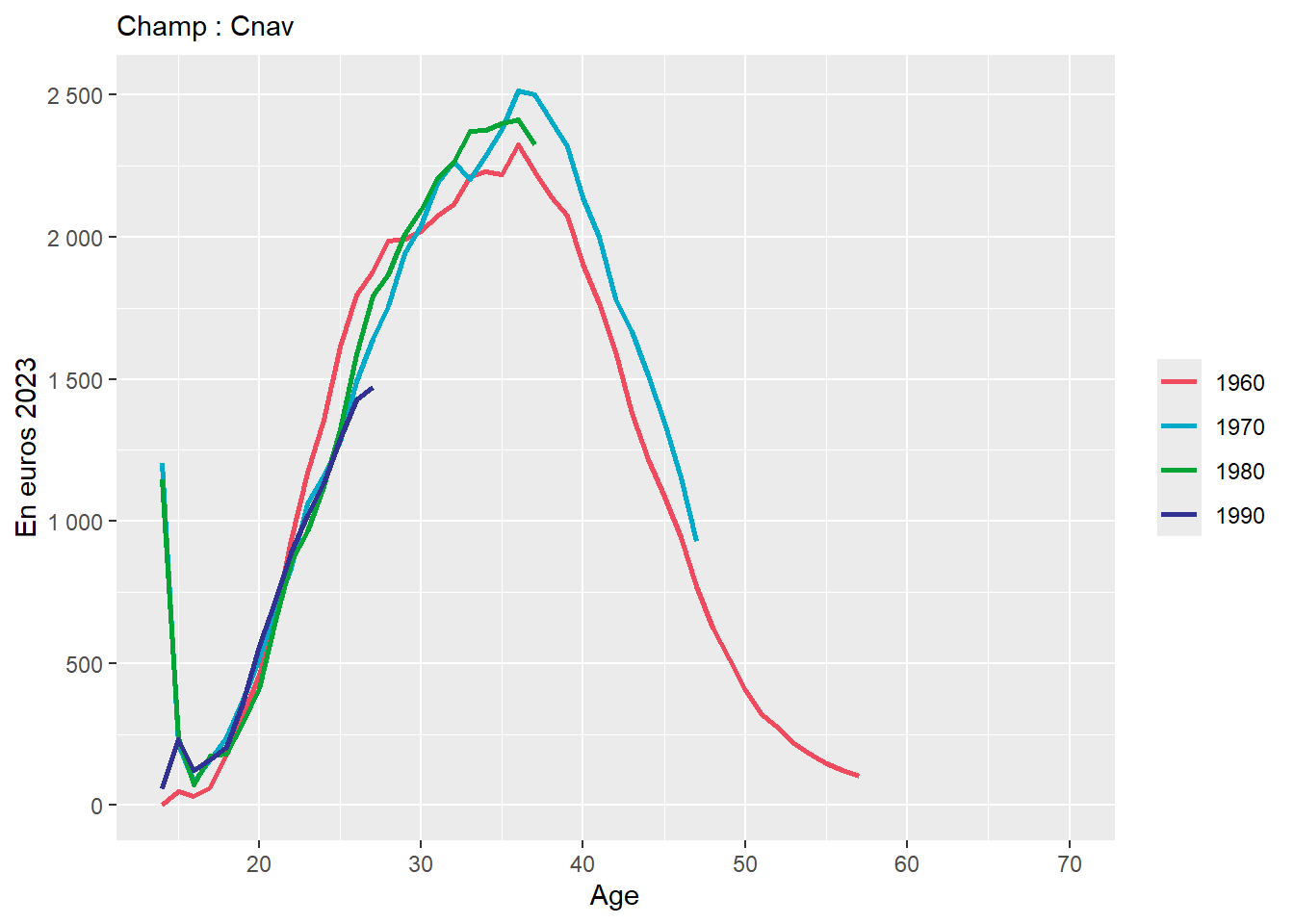
Le même alea est utilisé pour imputer tous les trimestres gratuits. Pour un individu donné à une année donnée, ce choix ne pose pas de problème (un individu ne peut avoir qu’un seul état dans la liste Chômage principal, Chômage secondaire, Maladie principal, Maladie secondaire). Cependant, la probabilité d’obtenir des trimestres gratuits pour maladie ou pour chômage restera inchangée tout au long de la vie. Par conséquent, un individu fréquemment malade, sera souvent au chômage et aura beaucoup d’AVPF.
Les trimestres gratuits sont les premiers trimestres de la carrière à être imputés (les trimestres cotisés sont estimés par la suite). Aucun contrôle sur le nombre total de trimestres n’est donc effectué.
3.4 Imputation des trimestres cotisés
3.4.1 Description
L’étape 3.4 permet d’imputer un nombre de trimestres cotisés par caisse et par an, pour chaque individu. On décide d’écraser la valeur observée et d’imputer partout car, sinon, on peut avoir un problème, notamment lors de variantes (ex : on supprime les trimestres AVPF utiles mais ils restent dans la variable nbTrimCotises)
Le nombre de trimestres cotisés est calculé comme suit :
\[nbTrimCotises_a= \left\{\begin{array}{c} min\left(4, \left\lfloor\frac{remuneration_a}{salaireValidant_a}\right\rfloor\right) & \text{si } caisse \in E\\ 4 & \text{si MSA exploitant} \end{array} \right.\]
Avec :
\[E = \{Cnav, MSA Salarié, RSI base, CNAVPL\}\]
Chez les fonctionnaires, les trimestres cotisés dépendent de la durée calendaire travaillée et de la quotité. Ils sont calculés en amont, et intégrés dans dtIdAnCaisse à l’étape 2.34.
3.4.2 Résultats
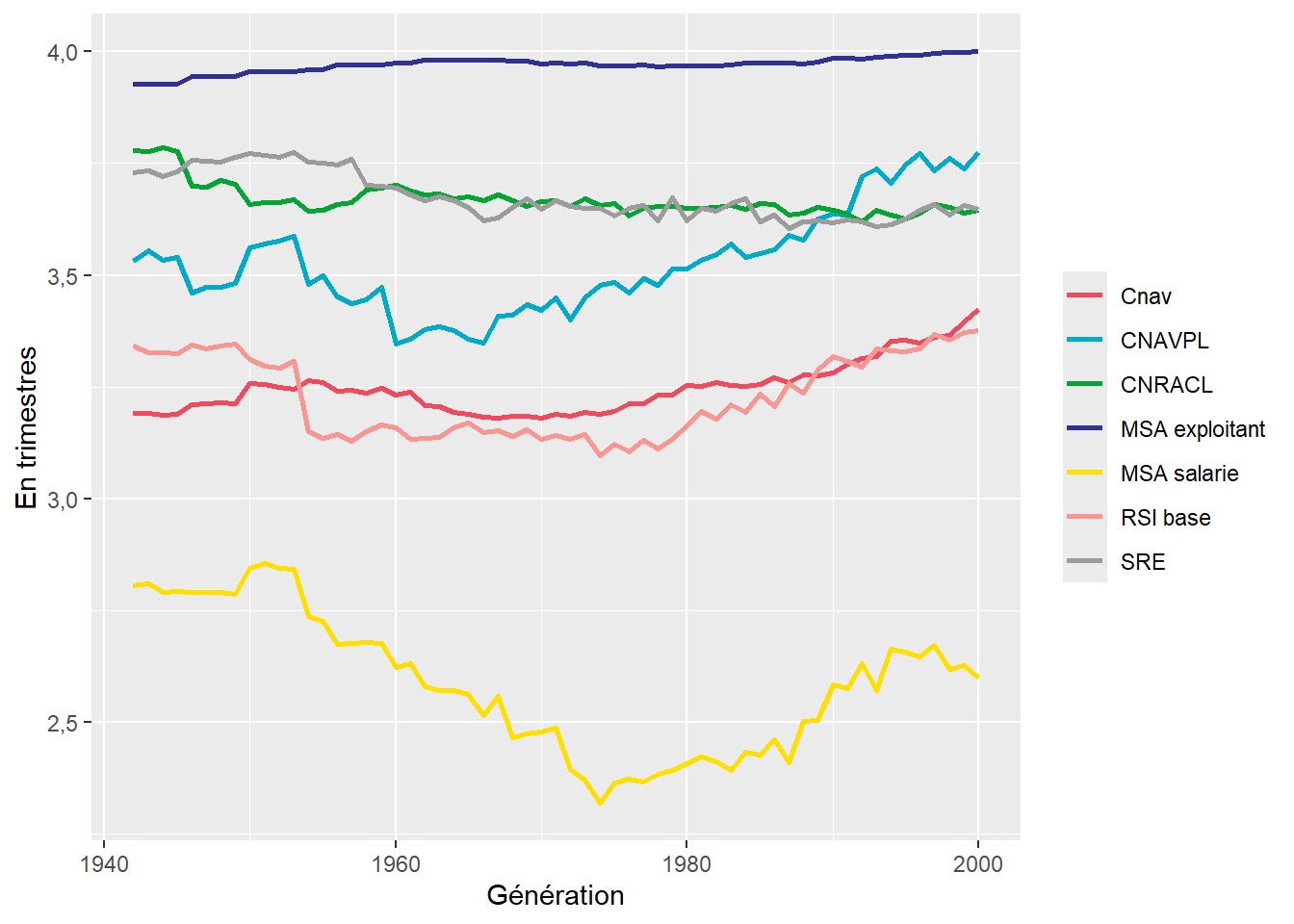
3.4.3 Calcul trimestres AVPF utiles
Dans le cadre des départs en carrière longue (et du calcul du Minimum contributif avant septembre 2023), il est nécessaire d’identifier les trimestres qui sont cotisés au titre de l’AVPF. Certains peuvent être “inutiles” si le nombre de trimestres cotisés via le travail permet déjà d’atteindre 4 trimestres dans l’année. Il faut donc conserver uniquement ceux qui augmentent la durée cotisée.
La base dtIdAnTrimAVPFUtile est ainsi créée.
3.5 Imputation des cotisations des régimes de base
3.5.1 Description
L’étape 3.5 permet de calculer le montant des cotisations pour les régimes de base, selon les formules suivantes :
3.5.1.2 MSA salarié
\[\begin{array}{l} cotisations_a^{salarié}=\\ \qquad min(remuneration_a, PSS_a) \times txCotis_a^{salarié,≤1PSS}\\ \qquad +remuneration_a \times txCotis_a^{salarié,déplafonné}\\ \\ cotisations_a^{employeur}=\\ \qquad min(remuneration_a, PSS_a) \times txCotis_a^{employeur, ≤1PSS}\\ \qquad +remuneration_a \times txCotis_a^{employeur, déplafonné} \end{array}\]
3.5.1.3 SRE
\[\begin{array}{ll} cotisations_a^{salarié} &=remuneration_a \times txCotis_a^{salarié}\\ cotisations_a^{employeur} &=remuneration_a \times txCotis_a^{employeur} \end{array}\]
3.5.1.4 CNRACL
\[\begin{array}{ll} cotisations_a^{salarié} &=remuneration_a \times txCotis_a^{salarié}\\ cotisations_a^{employeur} &=remuneration_a \times txCotis_a^{employeur} \end{array}\]
3.5.1.5 Régimes spéciaux
\[cotisations_a^{salarié}=remuneration_a \times txCotis_a^{salarié}\]
\[cotisations_a^{employeur}=remuneration_a \times \left(txCotis_a^{employeur, 1} + txCotis_a^{employeur, 2}\right)\]
3.5.1.7 RSI
\[\begin{array}{l} cotisations_a=\\ \qquad max(5,25\%PSS, min(remuneration_a, PSS_a)) \times txCotis_a^{≤1PSS}\\ \qquad +remuneration_a \times txCotis_a^{déplafonné} \end{array}\]
3.5.1.8 MSA exploitant
\[\begin{array}{l} cotisations_a=\\ \qquad max(800SMIC_a^{horaire}, min(remuneration_a, PSS_a)) \times txCotis^{≤1PSS, 1}\\ \qquad +max(600SMIC_a^{horaire}, min(remuneration_a, PSS_a)) \times txCotis^{≤1PSS, 2}\\ \qquad +max(600SMIC_a^{horaire}, remuneration_a) \times txCotis^{déplafonné} \end{array}\]
3.5.2 Résultats
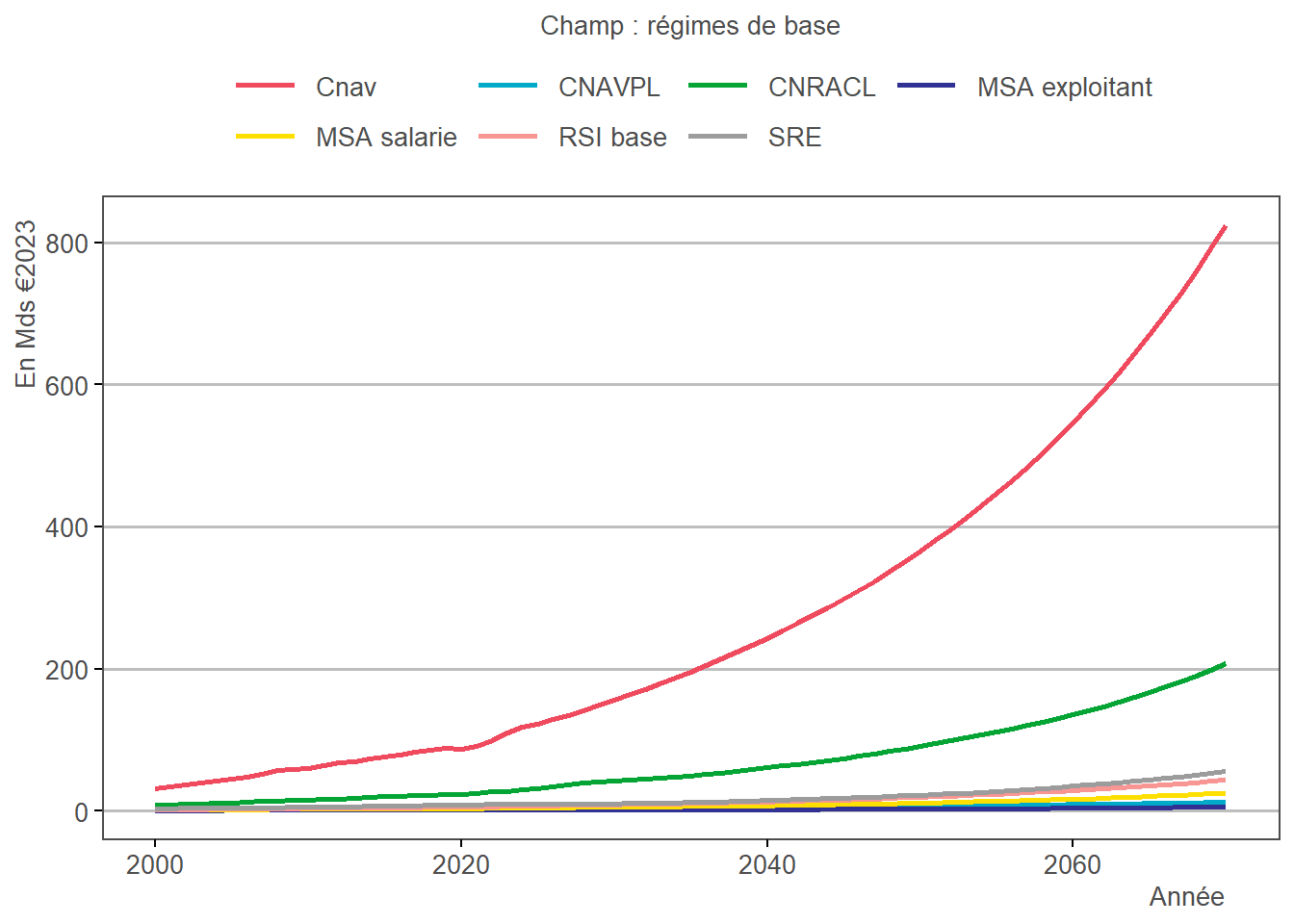
3.5.3 Discussion
En théorie, les cotisations employeur sont calculées sur du salaire super brut. Ici, on calcule les cotisations employeur à partir du brut.
3.6 Imputation des cotisations des régimes complémentaires
3.6.1 Description
L’étape 3.6 permet de calculer le montant des cotisations pour les régimes complémentaires, selon les formules suivantes :
3.6.1.1 Arrco (et Agirc-Arrco, sans Agirc)
\[\begin{array}{l} cotisations_a^{salarié}=\\ \qquad min(remuneration_a, PSS_a) \\ \qquad \times \left(txCotis_a^{salarié,≤PSS} \times tauxAppel_a + txCotis_a^{salarié, AGFF, ≤PSS}\right)\\ \\ cotisations_a^{employeur} = \\ \qquad min(remuneration_a, PSS_a) \\ \qquad \times \left(txCotis_a^{employeur,≤PSS} \times tauxAppel_a + txCotis_a^{employeur, AGFF, ≤PSS}\right) \end{array}\]
3.6.1.2 Agirc
\[\begin{array}{l}cotisations_a^{salarié}=\\ \qquad remuneration_a \times txCotis^{salarié,CET}\\ \qquad +min(max(0,salaireCharniere_a-PSS_a, remuneration_a-PSS_a), (4-1)PSS_a) \\ \qquad \qquad \times \left(txCotis_a^{salarié,]1PSS,4PSS]} \times tauxAppel_a + txCotis_a^{salarié, AGFF, ]1PSS,4PSS]}\right)\\ \qquad +min(max(0, remuneration_a-4PSS_a), (8-4)PSS_a) \\ \qquad \qquad \times \left( txCotis_a^{salarié, ]4PSS,8PSS]} \times txAppel_a+txCotis^{salarié, AGFF} \right)\\ \\ cotisations_a^{employeur}=\\ \qquad remuneration_a \times txCotis^{employeur,CET}\\ \qquad +min(max(0,salaireCharniere_a-PSS_a, remuneration_a-PSS_a), (4-1)PSS_a) \\ \qquad \qquad \times \left( txCotis_a^{employeur,]1PSS,4PSS]} \times tauxAppel_a + txCotis_a^{employeur, AGFF, ]1PSS,4PSS]}\right)\\ \qquad +min(max(0, remuneration_a-4PSS_a), (8-4)PSS_a) \\ \qquad \qquad \times \left( txCotis_a^{employeur,]4PSS,8PSS]} \times txAppel_a+txCotis^{employeur, AGFF} \right) \end{array} \]
3.6.1.3 Agirc-Arrco (avec Agirc)
\[\begin{array}{l}cotisations_a^{salarié}=\\ \qquad min(remuneration_a, PSS_a) \\ \qquad \qquad \times \left(txCotis_a^{salarié,≤PSS} \times tauxAppel_a + txCotis_a^{salarié, AGFF, ≤PSS}\right)\\ \qquad +min(max(0,remuneration_a-PSS_a), (plafond_a^{>PSS}-1) \times PSS_a) \\ \qquad \qquad \times \left( txCotis_a^{salarié, >PSS} \times txAppel_a \times txCotis_a^{salarié, AGFF, >PSS} \right)\\ \\ cotisations_a^{employeur} = \\ \qquad min(remuneration_a, PSS_a) \\ \qquad \qquad \times \left(txCotis_a^{employeur,≤PSS} \times tauxAppel_a + txCotis_a^{employeur, AGFF, ≤PSS}\right)\\ \qquad +min(max(0, remuneration_a-PSS_a), (3-1)PSS_a) \\ \qquad \qquad \times \left( txCotis_a^{employeur,]1PSS,3PSS]} \times txAppel_a + txCotis_a^{employeur, AGCC, ]1PSS,3PSS]} \right) \end{array}\]
3.6.1.4 Rafp
\[\begin{array}{l} cotisations_a^{salarié}=min(20\% \times remuneration_a, primes_a) \times txCotis_a^{salarié}\\ cotisations_a^{employeur}=min(20\% \times remuneration_a, primes_a) \times txCotis_a^{employeur} \end{array}\]
3.6.1.5 Ircantec
\[\begin{array}{l} cotisations_a^{salarié}=\\ \quad min(remuneration_a, PSS_a) \times txCotis_a^{salarié, ≤PSS} \times txAppel_a\\ \quad +min\left(max(0, remuneration_a-PSS_a), \left(plafond_a^{>PSS}-1\right)\times PSS_a\right) \\ \quad \quad \times txCotis_a^{salarié, >PSS} \times txAppel_a\\ \\ cotisations_a^{employeur}=\\ \qquad min(remuneration_a, PSS_a) \times txCotis_a^{employeur, ≤PSS} \times txAppel_a\\ \qquad +min\left(max(0, remuneration_a-PSS_a), \left(plafond_a^{>PSS}-1\right)\times PSS_a\right) \\ \qquad \qquad \times txCotis_a^{employeur, >PSS} \times txAppel_a \end{array}\]
3.6.1.6 CARMF
3.6.1.6.1 Complémentaire
\[cotisations_a = min(max(0, remuneration_a), 3,5PSS_a) \times txCotis_a\]
3.6.1.6.2 Supplémentaire
\[cotisations_a=\left\{\begin{array}{cl} \begin{array}{c}min(remuneration_a, 6\%PSS_a) \times txCotis_a \\ + 1{\{remuneration_a>0\}} \times 17\%PSS_a \end{array} & \text{si } a>2014\\ 0 & \text{sinon} \end{array}\right.\]
3.6.1.7 RSI
\[\begin{array}{l} cotisations_a=\\ \qquad min(remuneration_a, PSS_a) \times txCotis_a^{≤PSS}\\ \qquad +min(max(0,remuneration_a-PSS_a),(3-1)PSS_a) \times txCotis_a^{]1PSS,4PSS]} \end{array}\]
3.6.1.8 MSA exploitant
\[\begin{array}{l} cotisations_a=max(remuneration_a,600\times SMIC_a^{horaire}) \times txCotis_a \end{array}\]
3.6.2 Résultats
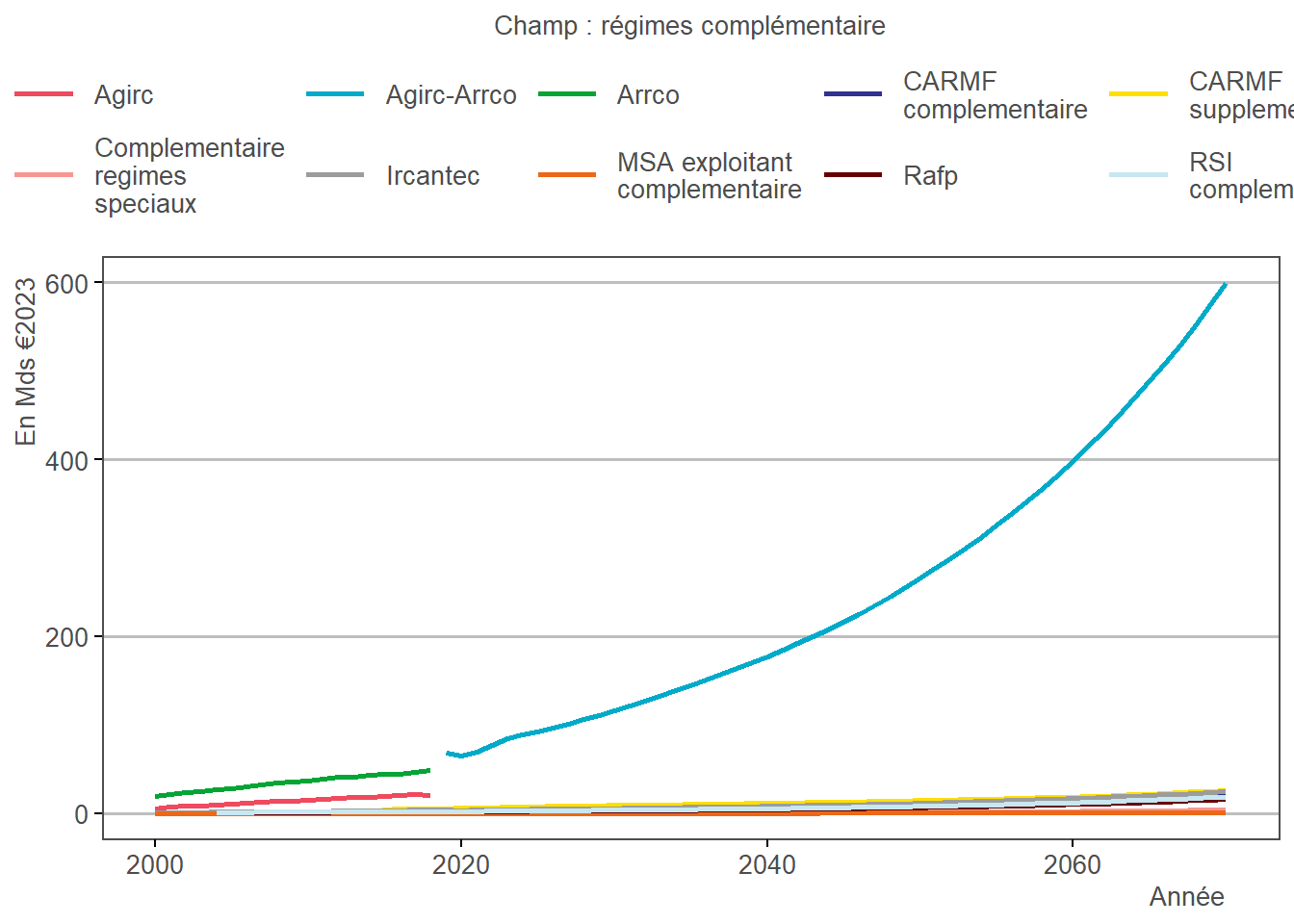
3.7 Imputation des points cotisés pour les régimes complémentaires
3.7.1 Description
L’étape 3.7 permet de calculer le nombre de points cotisés pour les régimes complémentaires, selon les formules suivantes :
3.7.1.1 Agirc
\[\begin{array}{l} nbPtCotises_a = \\ \qquad \left\{ \begin{array}{cl} \frac{cotisations_a}{valeurAcquisition_a} &\text{si }remuneration_a > salaireCharniere_a\\ garantieMinimale_a \times \frac{nbTrimCotise_a}{4}&\text{sinon} \end{array} \right. \end{array}\]
Avec :
\[\begin{array}{l} cotisations_a = \\ \qquad \begin{array}{l} min(max(0, salaireCharniere_a-PSS_a,remuneration_a-PSS_a), (4-1)PSS_a) \\ \qquad \times \left( txCotis_a^{salarié, ]1PSS, 4PSS]} + txCotis_a^{employeur, ]1PSS, 4PSS]} \right) \\ +min(max(0,remuneration_a-4PSS_a), (8-4)PSS_a) \\ \qquad \times \left( txCotis_a^{salarié, ]4PSS, 8PSS]} + txCotis_a^{employeur, ]4PSS, 8PSS]} \right) \end{array} \end{array}\]
3.7.1.2 CARMF
3.7.1.2.1 Complémentaire
\[\begin{array}{l} nbPtsCotises_a = \\ \qquad \left\{ \begin{array}{cl} arrondi\left(\frac{4}{3} \times nbTrimCotises_a \right) & \text{si } annee< 1983\\ arrondi\left( \frac{4}{3} \times \left( nbTrimCotises_a+arrondi\left(\frac{cotisations_a}{valeurAcquisitionPt_a}\right)\right) \right)& \text{si } annee< 1991\\ nbTrimCotises_a + arrondi\left(\frac{cotisations_a}{valeurAcquisitionPt_a}\right) & \text{si } annee< 1996\\ arrondi\left(min\left(\frac{remuneration_a}{valeurAcquisitionPt_a},\frac{3,5PSS_a}{valeurAcquisitionPt_a}, 10\right)\right) & \text{sinon } \end{array}\right. \end{array}\]
Avec :
\[cotisations_a = min(max(plancher_a, remuneration_a),plafond_a) \times txCotis_a\]
3.7.1.2.2 Supplémentaire
Note : sauf erreur, il y a une simplification par arrondi(forfaitASV*nbTrimCotises/4)
\[nbPtsCotises_a = \left\{ \begin{array}{cl} arrondi\left(forfaitASV_a \times \frac{nbTrimCotises}{4}\right) &\text{si } annee < 2012\\ \begin{array}{c} arrondi\left(forfaitASV_a \times \frac{nbTrimCotises}{4}\right) \\ + arrondi\left(min\left( \frac{txCotis_a \times min(remuneration_a, 5PSS_a) \times \frac{2}{3}}{valeurAcquisitionPt_a},9 \right)\right)\end{array} &\text{si } nbTrimCotises > 0\\ 0 &\text{sinon} \end{array}\right.\]
3.7.1.3 Arrco et Agirc-Arrco sans Agirc
\[nbPtsCotises_a = \frac{min(remuneration_a, PSS_a) \times \left( txCotis_a^{salarié} + txCotis_a^{emloyeur} \right)}{valeurAcquisitionPt_a}\]
3.7.1.4 Agirc-Arrco
\[nbPtsCotises_a = \frac{cotisations_a}{valeurAcquisitionPt_a} \] Avec :
\[\begin{array}{l} cotisations_a = \\ \qquad min(remuneration_a, PSS_a) \times \left( txCotis_a^{salarié, ≤PSS} + txCotis_a^{emloyeur, ≤PSS} \right) \\ \qquad + min\left(max(0,remuneration_a-PSS_a),\left( plafond_a^{>PSS}-1 \right) \times PSS_a \right) \\ \qquad \qquad \times \left( txCotis_a^{salarié, >PSS} + txCotis_a^{emloyeur, >PSS} \right) \end{array}\]
3.7.1.5 MSA exploitant
\[nbPtsCotises_a = \left\{ \begin{array}{cl} 100 &\text{si } remuneration_a ≤ 1820 \times SMIC_a^{horaire}\\ 100 \times \frac{remuneration_a}{1820 \times SMIC_a^{horaire}} & \text{sinon} \end{array} \right.\]
3.7.1.6 Ircantec
\[nbPtsCotises_a = \frac{\frac{cotisations_a^{salarié}}{txAppel_a} + cotisations_a^{employeur}}{valeurAcquisitionPt_a}\]
3.7.1.7 Rafp et RSI
\[nbPtsCotises_a = \frac{cotisations_a^{salarié}+cotisations_a^{employeur}}{valeurAcquisitionPt_a}\]
3.7.2 Résultats
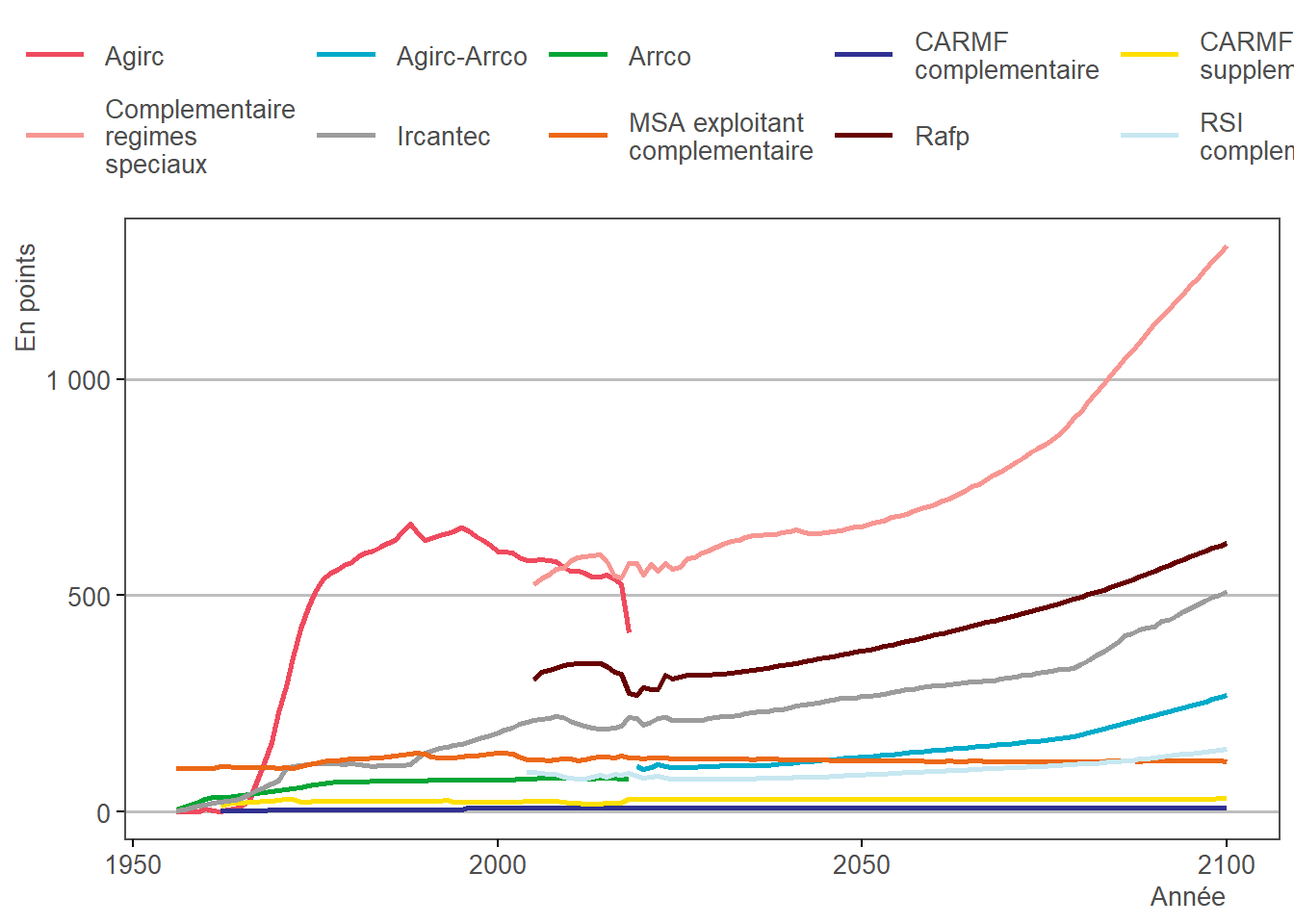
3.8 Calcul du nombre de points gratuits
3.8.1 Description
L’étape 3.8 permet de calculer le nombre de points gratuits (octroyés en cas d’arrêt maladie ou de chômage), en se basant sur les formules suivantes :
3.8.1.1 Arrco
\[\begin{array}{l} nbPtsGratuits_a = \\ \qquad \left\{ \begin{array}{cl} \begin{array}{c}\frac{nbTrimGratuits_a}{4} \\\times \frac{min(remuneration_{a-1},PSS_a) \times \left( txCotis_a^{salarié} + txCotis_a^{employeur} \right)}{valeurAcquisitionPt_a}\end{array} & \begin{array}{}\text{si } nbTrimGratuits_a^{chomage}>0 \\ \text{ et } remuneration_{a-1}>0 \end{array}\\ \begin{array}{c}\frac{nbTrimGratuits_a}{4} \times \frac{SMIC_a \times \left( txCotis_a^{salarié} + txCotis_a^{employeur} \right)}{valeurAcquisitionPt_a}\end{array} & \begin{array}{}\text{si } nbTrimGratuits_a^{chomage}>0 \\ \text{ et } remuneration_{a-1}=0 \end{array} \\ \begin{array}{c}\frac{nbTrimGratuits_a}{4} \\\times max(0,nbPtsCotises_{a-1}-nbPtsCotises_a)\end{array} & \begin{array}{}\text{si } nbTrimGratuits_a^{maladie}>0 \\\text{ et } remuneration_{a-1}>0 \end{array} \\ 0 & \text{sinon} \end{array}\right. \end{array}\]
3.8.1.2 Agirc
\[\begin{array}{l} nbPtsGratuits_a = \\ \qquad\left\{ \begin{array}{cl} \begin{array}{c}\frac{nbTrimGratuits_a}{4} \\\times max\left(\begin{array}{}garantieMinimale_a, \frac{cotisations_a}{valeurAcquisitionPt_a}\end{array}\right)\end{array} &\begin{array}{l}\text{si } remuneration_{a-1}>0 \\\qquad\text{et } nbTrimGratuits_a^{chomage}>0\end{array}\\ \begin{array}{c}\frac{nbTrimGratuits}{4} \\\times max\left(0, (nbPtsCotises_{a-1}-nbPtsCotises_a)\right)\end{array}& \begin{array}{l}\text{si } remuneration_{a-1}>0 \\\qquad\text{et } nbTrimGratuits_a^{maladie}>0\end{array}\\ \frac{nbTrimGratuits_a}{4} \times garantieMinimale_a &\text{si } remuneration_{a-1}=0 \\ 0 &\text{sinon} \end{array}\right. \end{array}\]
Avec :
\[\begin{array}{l} cotisations_a = \\ \qquad max(0, min(remuneration_{a-1} - PSS_a), (4-1)PSS_a) \\ \qquad\qquad\times \left( txCotis_a^{salarié, ]1PSS, 4PSS]} + txCotis_a^{employeur, ]1PSS, 4PSS]} \right)\\ \qquad+max(0,min(remuneration_{a-1}-4PSS_a, (8-4) \times PSS_a)) \\ \qquad\qquad\times \left( txCotis_a^{salarié, ]4PSS, 8PSS]} + txCotis_a^{employeur, ]4PSS, 8PSS]} \right) \end{array}\]
3.8.1.3 Agirc-Arrco
\[\begin{array}{l} nbPtsGratuits_a = \\ \qquad\left\{ \begin{array}{cl} \begin{array}{c} \frac{nbTrimGratuits_a}{4} \times \frac{cotisations_a^{<1PSS}}{valeurAcquisitionPt_a} \\ +1{\{Agirc\}} \times \frac{cotisations_a^{]1PSS, 3PSS]}}{valeurAcquisitionPt_a} \end{array} & \begin{array}{}\text{si } nbTrimGratuits_a^{chomage}>0 \\\qquad\text{et } remuneration_{a-1}>0 \end{array}\\ \frac{nbTrimGratuits_a}{4} \times \frac{SMIC_a \times \left( txCotis_a^{salarié} + txCotis_a^{employeur} \right)}{valeurAcquisitionPt_a} & \begin{array}{}\text{si } nbTrimGratuits_a^{chomage}>0 \\\qquad\text{et } remuneration_{a-1}=0\end{array} \\ \begin{array}{c}\frac{nbTrimGratuits_a}{4} \\\times max(0,nbPtsCotises_{a-1}-nbPtsCotises_a)\end{array} & \begin{array}{}\text{si } nbTrimGratuits_a^{maladie}>0 \\\qquad\text{et } remuneration_{a-1}>0 \end{array}\\ 0 & \text{sinon} \end{array}\right. \end{array}\]
Avec :
\[\begin{array}{l} cotisations_a^{<1PSS} = \\ \qquad min(remuneration_{a-1},PSS_a) \\ \qquad\times \left( txCotis_a^{salarié, <1PSS} + txCotis_a^{employeur, <1PSS} \right)\\ \\ cotisations_a^{]1PSS, 3PSS]} = \\ \qquad max\left(0,min\left(\frac{nbTrimGratuits_a}{4} \times remuneration_{a-1}-PSS_a\right), (3-1)PSS_a\right) \\ \qquad \times \left( txCotis_a^{salarié} + txCotis_a^{employeur} \right)\end{array}\]
3.8.1.4 CARMF
3.8.1.4.1 Complémentaire
\[\begin{array}{l} nbPtsGratuits_a = \\ \qquad\left\{ \begin{array}{cl} min(2 \times nbTrimGratuits_a,4) & \text{si } nbTrimGratuits_a^{maladie} > 0\\ 0 & \text{sinon} \end{array} \right. \end{array}\]
3.8.1.4.2 Supplémentaire
\[\begin{array}{l} nbPtsGratuits_a = \\ \qquad\left\{ \begin{array}{cl} arrondi(forfaitASV_a, \frac{nbTrimGratuits_a}{4}) & \text{si } nbTrimGratuits_a^{maladie} > 0\\ 0 & \text{sinon} \end{array} \right. \end{array}\]
3.8.1.5 Ircantec
\[nbPtsGratuits_a = \left\{ \begin{array}{cl} \begin{array}{c} \frac{cotisations_a}{valeurAcquisitionPt_a} \times \frac{nbTrimGratuits_a}{4} \end{array} & \begin{array}{l}\text{si } nbTrimGratuits_a > 0 \\\qquad\text{et } remuneration_{a-1} > 0\end{array} \\ \frac{nbTrimGratuits_a}{4} \times \frac{SMIC_a \times txCotis_a}{valeurAcquisitionPt_a} & \begin{array}{l}\text{si } nbTrimGratuits_a = 0 \\\qquad\text{et } remuneration_{a-1} > 0\end{array} \\ 0 & \text{sinon} \end{array}\right.\]
Avec :
\[\begin{array}{l} cotisations_a = \\ \qquad min(remuneration_{a-1},PSS_a) \times txCotis_a^{≤PSS} \\ \qquad + max\left(0,min(remuneration_{a-1}-PSS_a, (plafond_a-1)PSS_a)\right) \times txCotis_a^{>PSS} \end{array}\]
3.8.1.6 MSA exploitant
\[\begin{array}{l} nbPtsGratuits = \\ \qquad max\left(0, min\left(37,5, nbAnneesExploitant^{avant2003}\right) - nbAnneesExploitant^{apres2003}\right) \\ \qquad \times 100 \end{array}\]
3.8.1.7 RSI et Rafp
\[nbPtsGratuits_a = \left\{ \begin{array}{cl} 24 & \text{si } nbTrimGratuits_a^{maladie} > 0\\ 0 & \text{sinon} \end{array}\right.\]
3.8.2 Résultats
La fusion de l’Agirc et de l’Arrco apporte beaucoup moins de points gratuits en moyenne aux salariés du privé. En effet, il existait auparavant une garantie minimale de points à l’Agirc, qui permettait aux cadres d’obtenir au minimum 120 points gratuits jusqu’en 2019, année de la fusion.
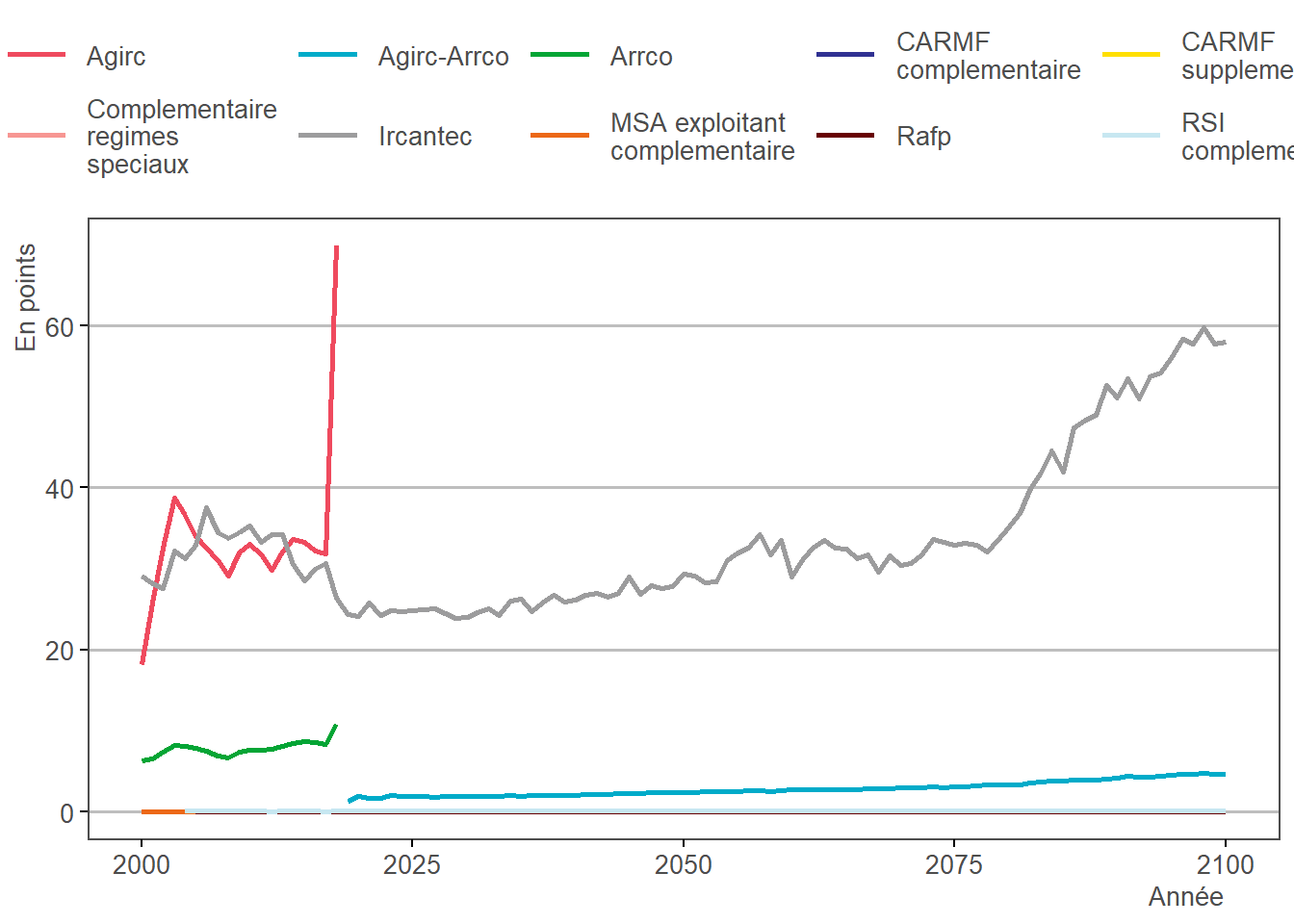
3.9 Calcul des rémunérations nettes
Les rémunérations nettes doivent être calculées pour obtenir les taux de remplacement nets. Pour cela, on utilise les taux de cotisations importés dans les paramètres COR à l’étape 1.7.
3.10 Calcul des primes nettes
Une étape spécifique calcule les cotisations à la Retraite Additionnelle de la Fonction Publique (RAFP). Dans ce régime, l’assiette de cotisation correspond aux primes des fonctionnaires (dans la limite de 20 % du traitement indiciaire brut).
On obtient donc les primes nettes, qui permettront là aussi de calculer plus tard les taux de remplacement nets.
3.11 Calcul des trimestres validés
3.11.1 Description
L’étape 3.11 permet de calculer le nombre de trimestres validés, selon la formule suivante :
\[nbTrimValides_a= min(nbTrimCotises_a + nbTrimGratuits_a, 4)\]
3.11.2 Résultats
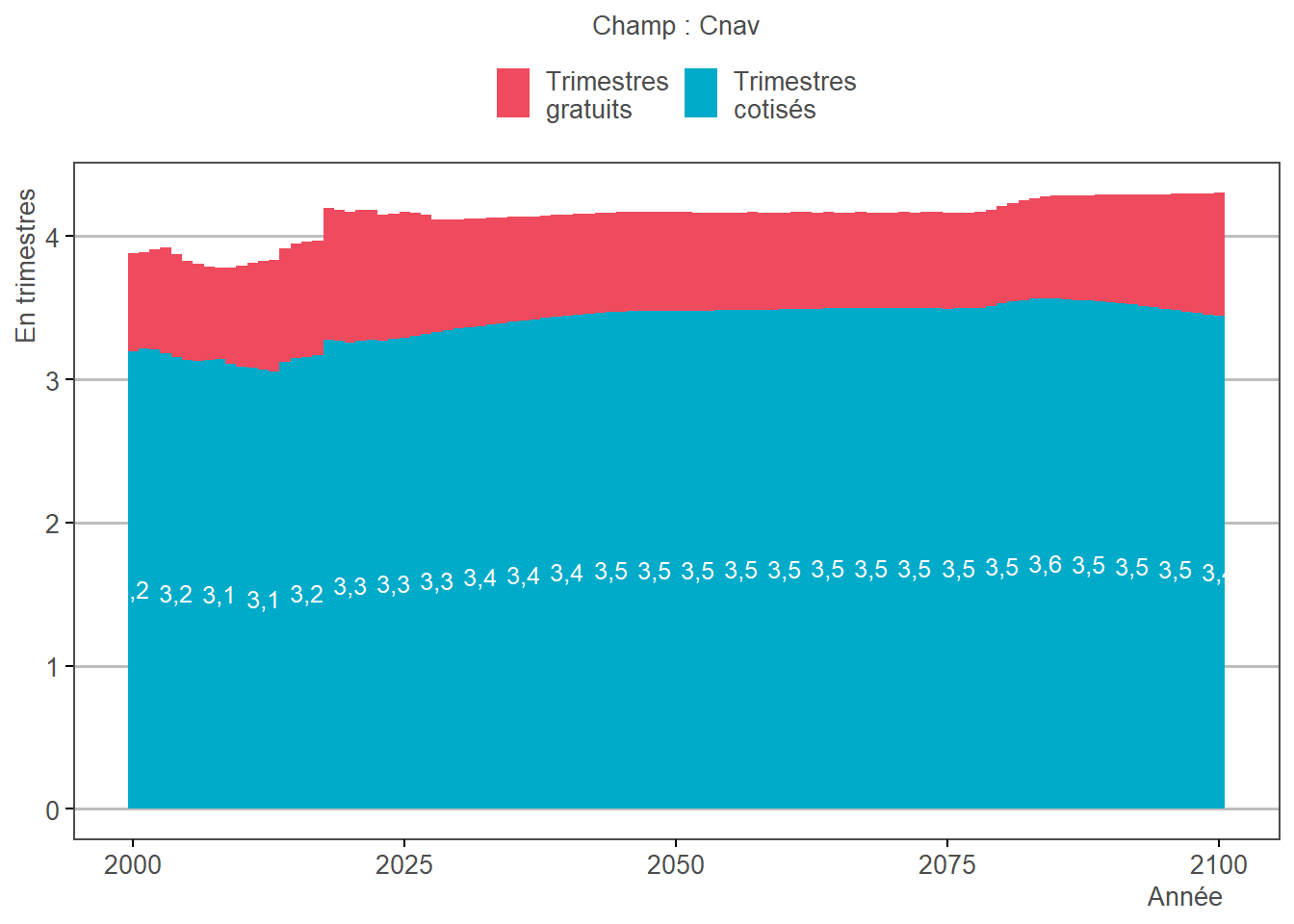
3.12 Imputation de la catégorie au sein de la fonction publique
3.12.1 Description
L’étape 3.12 permet d’imputer une catégorie au sein de la fonction publique (sédentaire, actif, super-actif). Par hypothèse, un individu ne peut avoir qu’une seule catégorie de fonction publique associée à une caisse pour l’ensemble de sa carrière.
Pour rappel, l’imputation de la catégorie au sein de la fonction publique repose sur la distribution calculée à l’étape 1.18 :
3.12.2 Résultats
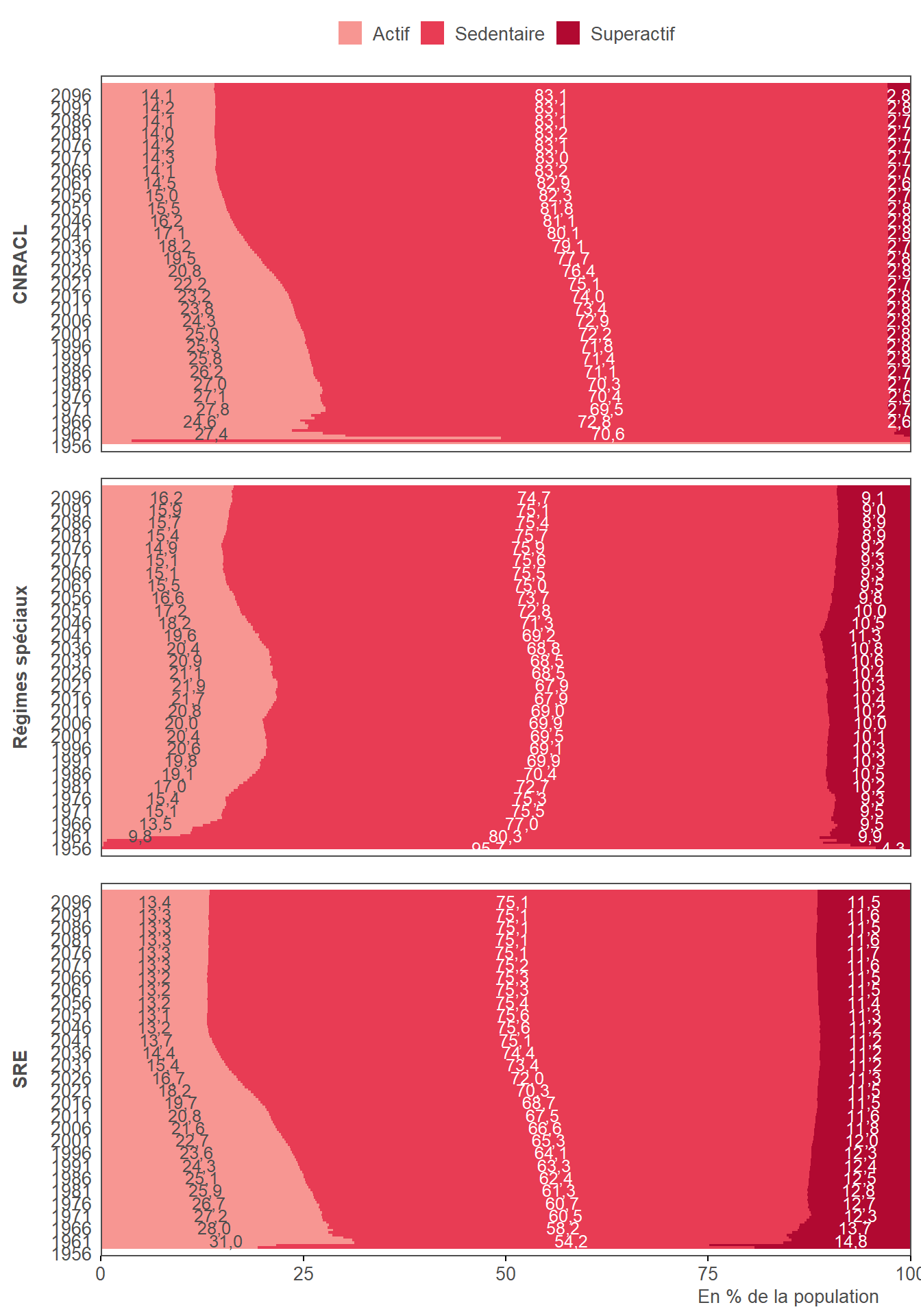
3.13 Imputation du nombre d’enfants
3.13.1 Description
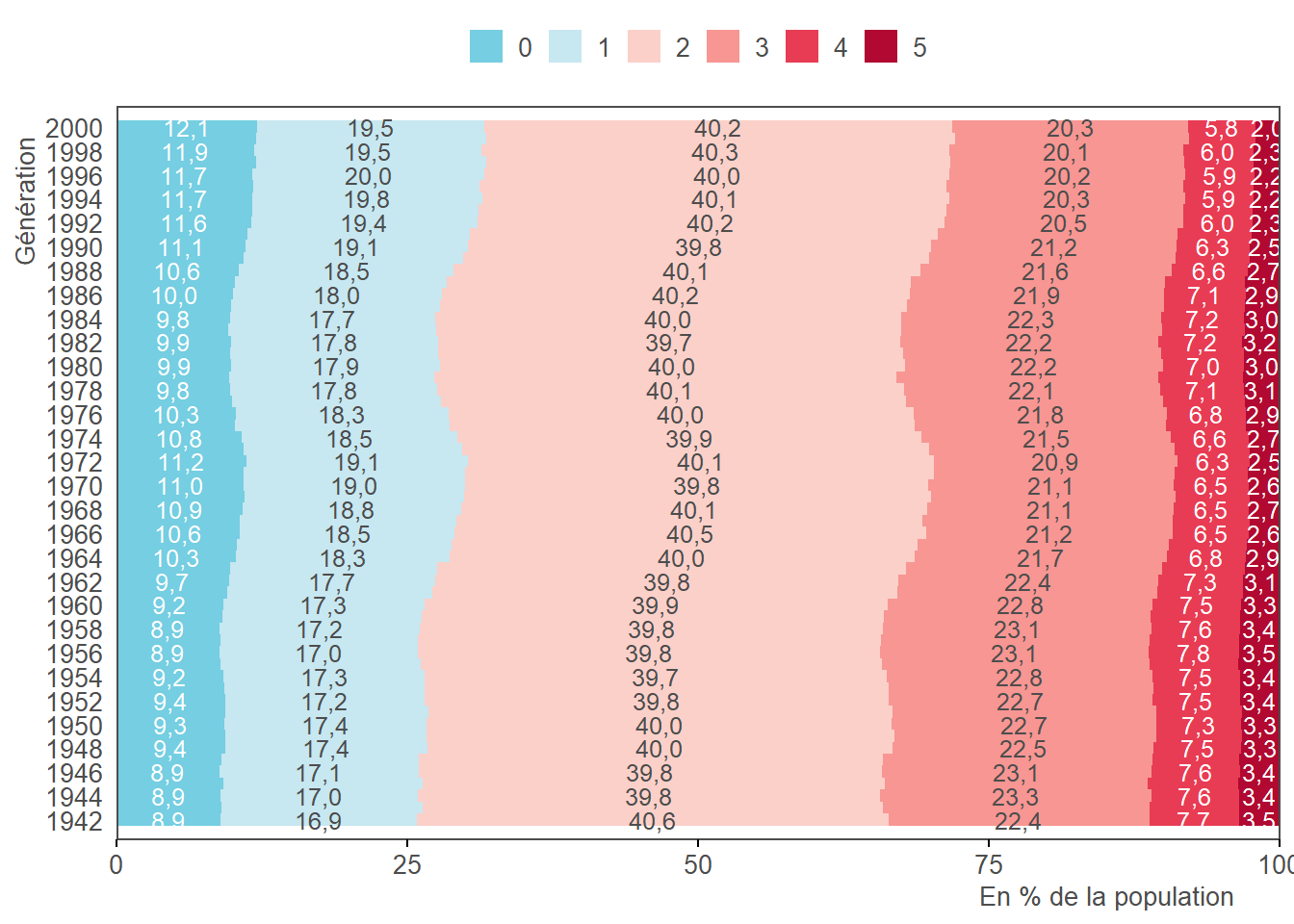
L’étape 3.13 permet d’imputer un nombre d’enfants par individu (de 0 à 5 au maximum). Dans un premier temps, la distribution générique de nombre d’enfants (calculée à l’étape 1.8) est importée :
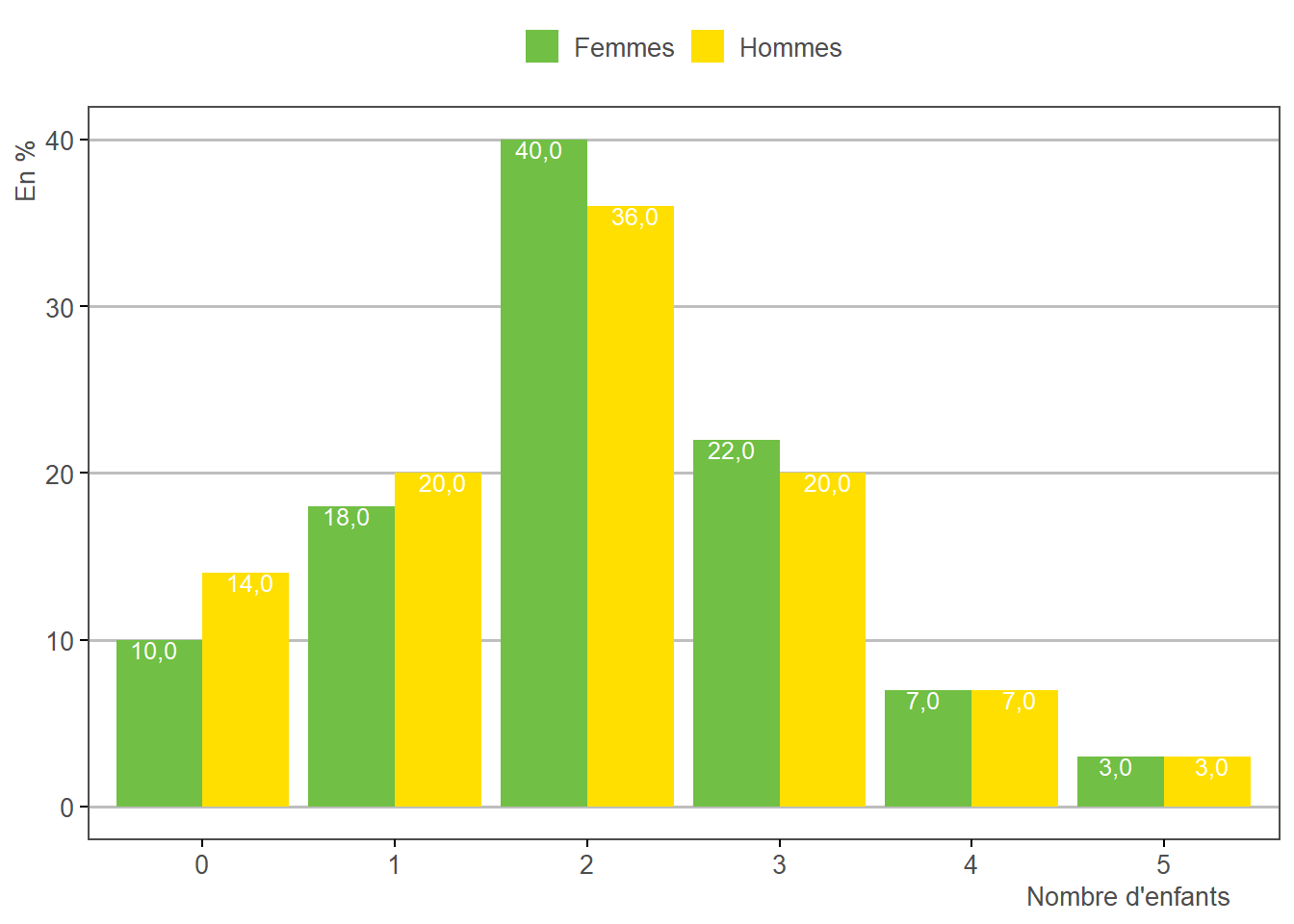
Cette distribution est ensuite déformée par calage sur marge via un nombre moyen d’enfants par individu (calculé à l’étape 1.8), afin d’obtenir une distribution spécifique à chaque génération et à chaque sexe :
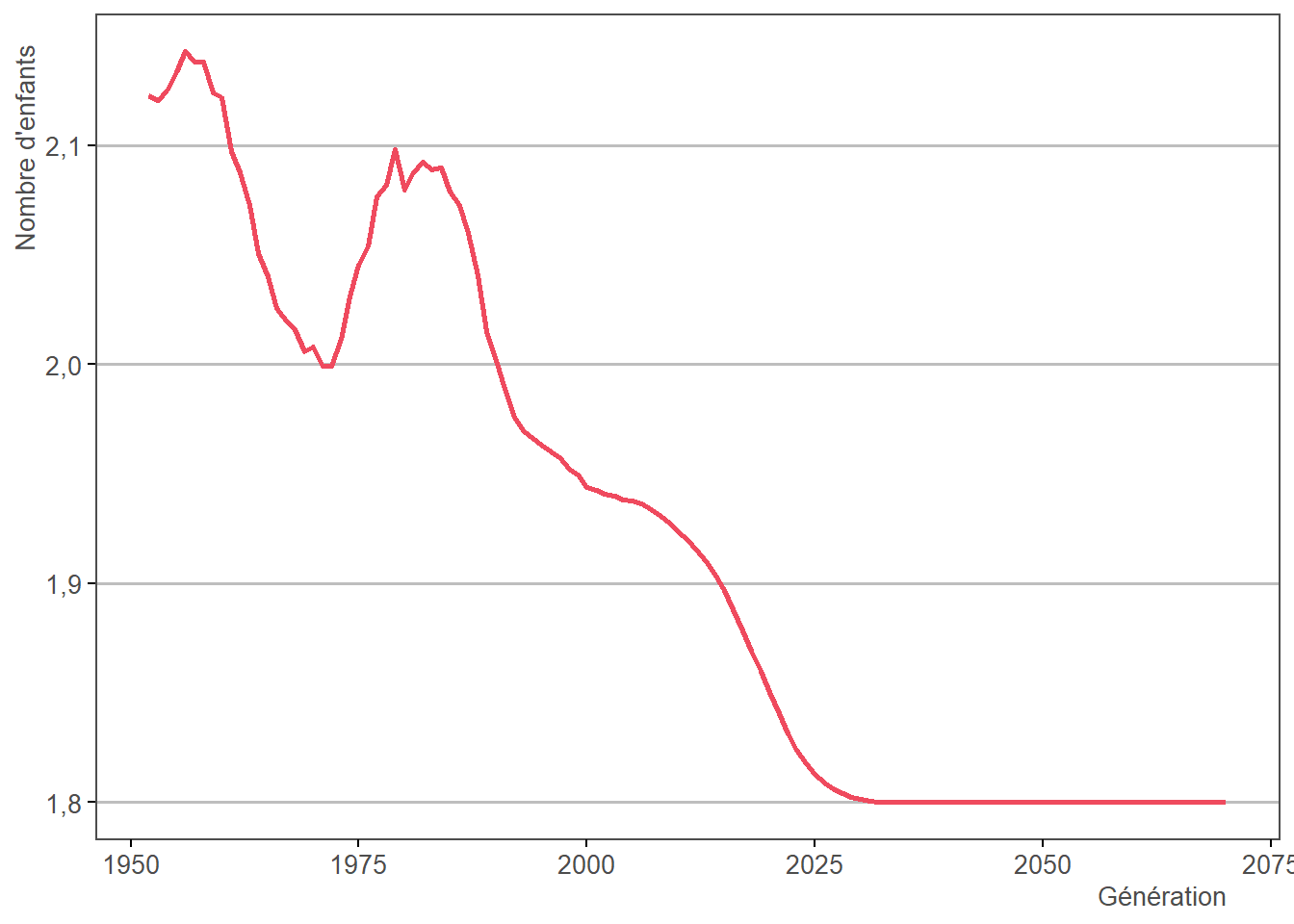
Le nombre d’enfants par individu est par la suite imputé en fonction d’un tirage aléatoire, dépendant du nombre de trimestres d’AVPF de l’individu (il est fait l’hypothèse que le nombre de trimestres d’AVPF d’un individu est corrélé à son nombre d’enfants). L’aléa individuel utilisé pour le tirage est défini comme suit :
\[alea_i = \frac{rang_i^{gen}}{maxRang^{gen}}\]
Avec :
\[maxRang^{gen} = max\left(\left\{rang_i^{gen} \forall i | gen_i=gen \right\}\right)\]
\[rang_i^{gen} = rang(score_i^{gen}))\]
Et :
\[score_i^{gen} = nbTrim_i^{AVPF} + \left(1+nbMaxTrim^{AVPF, gen}\right) \times \mathcal{U}_{[0, 1]}\]
\[nbMaxTrim^{AVPF, gen} = max\left(\left\{nbTrim_i^{AVPF} \forall i |gen_i = gen \right\}\right)\]
Ainsi, un individu avec un \(alea_i\) proche de 0 aura 0 enfants. Un individu avec un \(alea\) proche de 1 aura 5 enfants.
3.13.2 Résultats
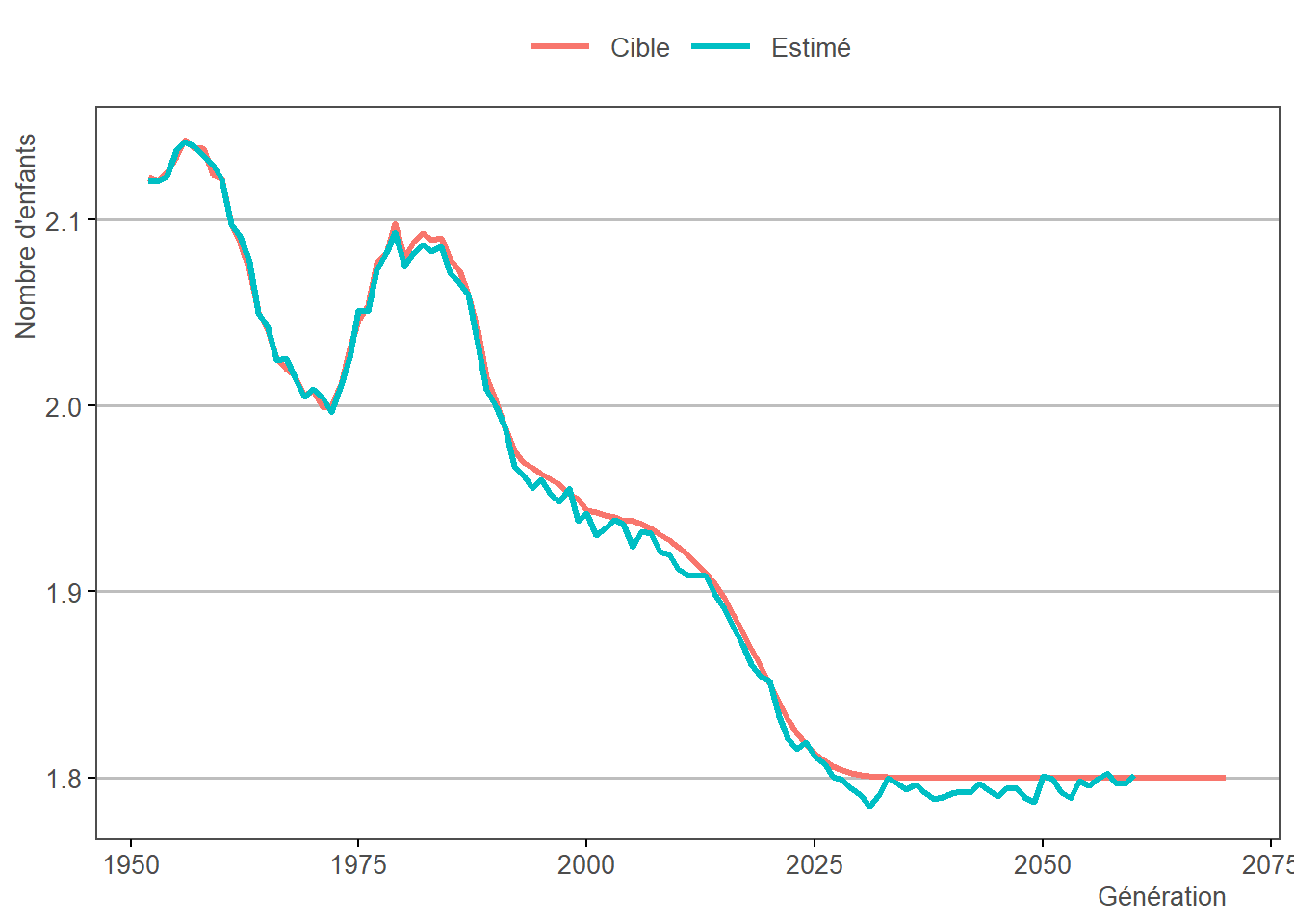
Note > Estimé = Après callage sur marge
3.14 Imputation des âges auxquels les individus ont leurs enfants
3.14.1 Description
L’étape 3.14 permet d’imputer l’âge auquel les individus auront leurs enfants par tirage aléatoire effectué à partir de la distribution calculée à l’étape 1.8. Pour tous les couples sexe * nombre d’enfants, on associe à chaque combinaison d’âges possibles de naissance des enfants une probabilité (voir ci-dessous). Dès lors, l’aléa “Naissance enfants” de chaque individu permet de déterminer la combinaison qui lui est imputée.
3.14.2 Résultats
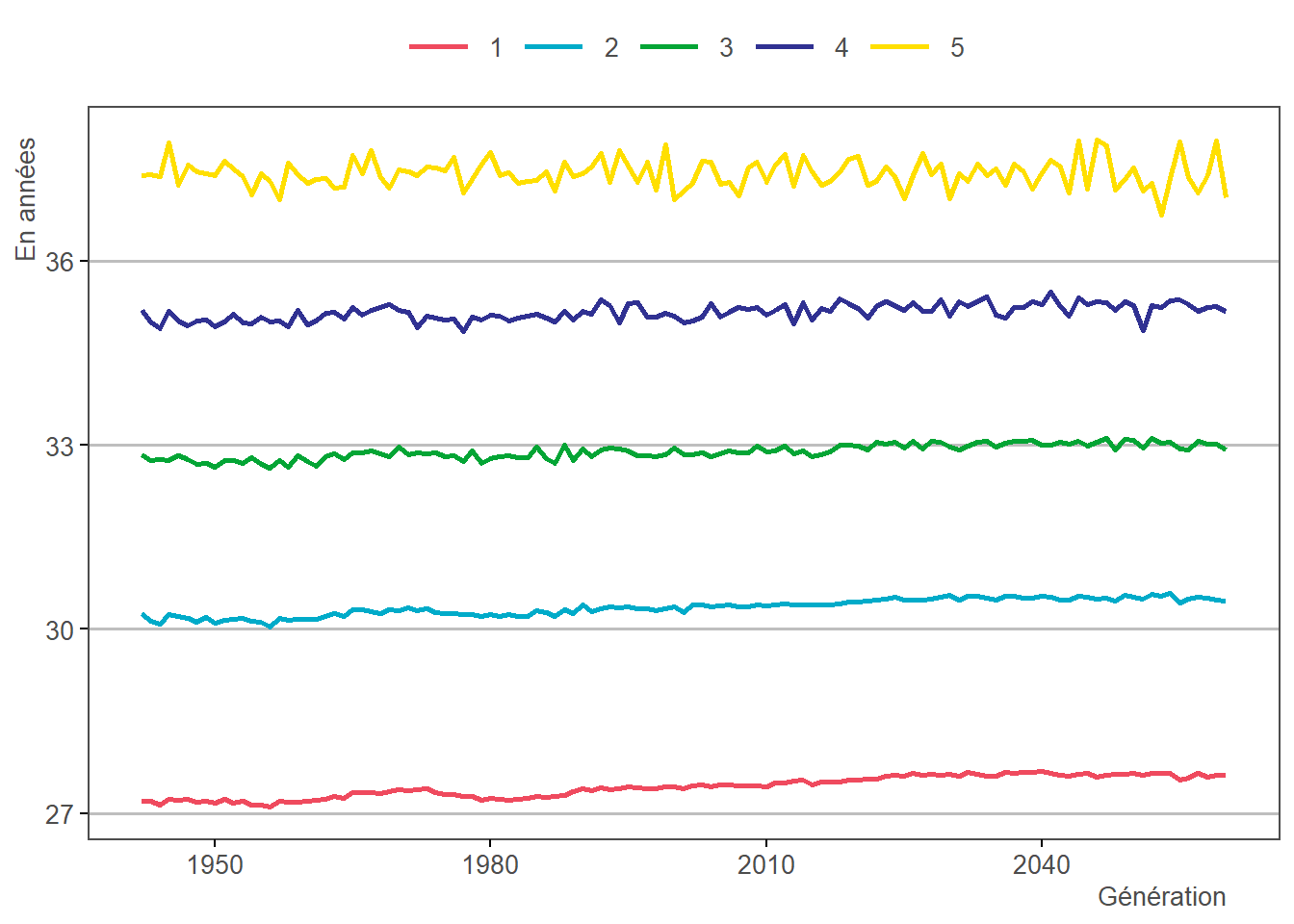
3.15 Imputation des jours d’invalidité/chômage/maladie/maternité/emploi
Étape en chantier (callout-caution pour le qmd)
3.16 Imputation des points cotisés pour les régimes de base
3.16.1 Description
L’étape 3.16 permet de calculer un nombre de points pour les régimes de base selon les formules suivantes :
3.16.1.1 RSI
Note : Le RSI n’est plus un régime en points depuis 1973.
3.16.1.2 MSA exploitants
\[\begin{array}{l}nbPts_a = \\ \qquad \left\{ \begin{array}{cl} 0 &\text{si }remuneration_a=0\\ 23 &\text{si }remuneration_a≤600SMIC_a^{horaire}\\ min\left( 23 + \frac{7 \times (remuneration_a-600SMIC_a^{horaire})}{800SMIC_a^{horaire}-600SMIC_a^{horaire}}, 30 \right) &\text{si }remuneration_a≤800SMIC_a^{horaire}\\ 30 &\text{si }remuneration_a ≤2MICO_a\\ 30 + max\left( 0, \frac{(nbMaxPts_a-30)(remuneration_a-2MICO_a)}{salaireValidant_a-2MICO_a} \right) &\text{si }remuneration_a<salaireValidant_a\\ 1+max(30,nbMaxPts_a) &\text{si }remuneration_a≥salaireValidant_a \end{array}\right. \end{array}\]
Avec :
\[nbMaxPts_a = max\left(\left\lfloor\frac{50\%\times salaireValidant_a - montantAvts_a}{37,5 \times valeurPoint_a}\right\rfloor, 30\right)\]
3.16.2 Résultats
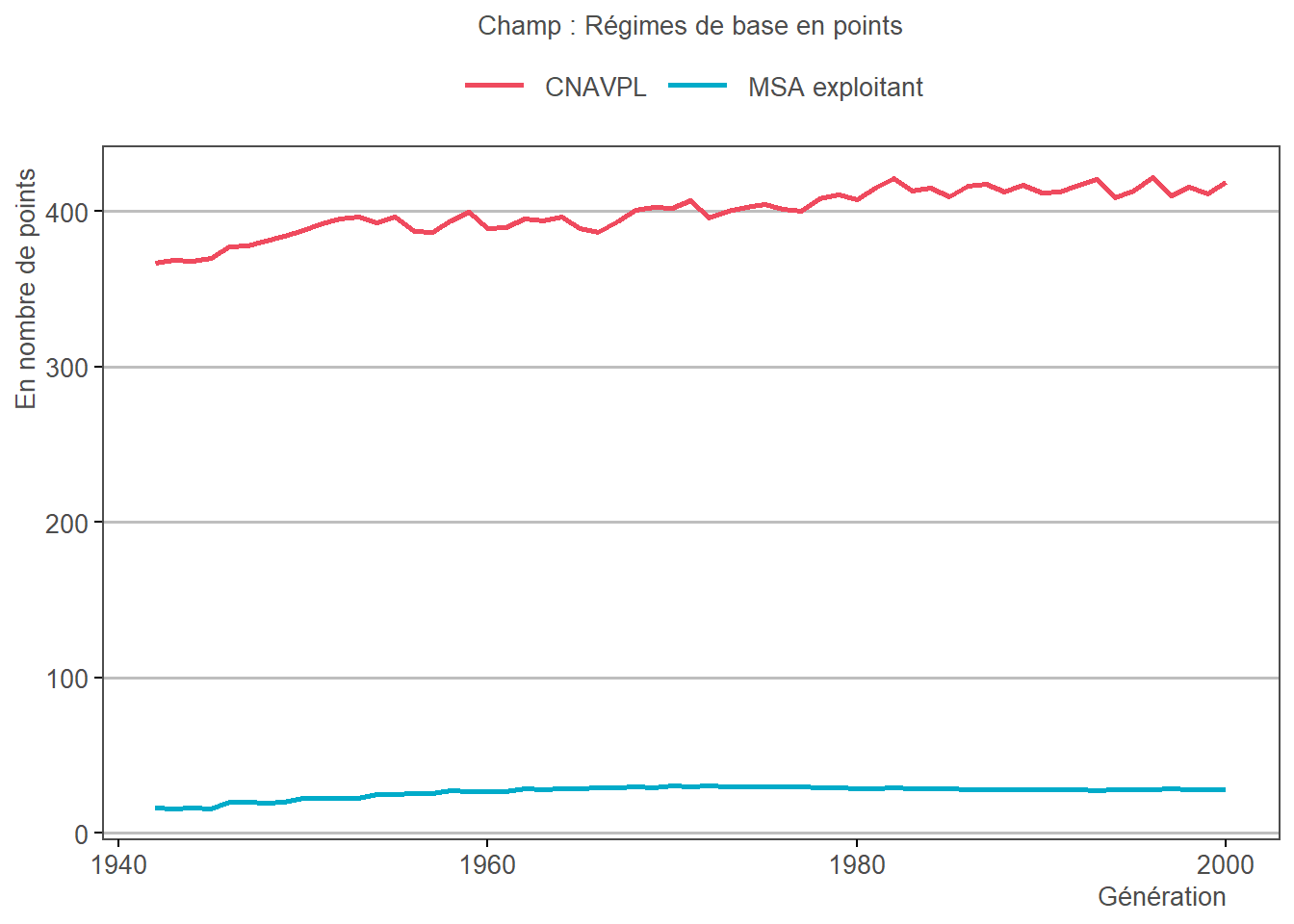
3.17 Calcul du nombre total de points
La section permet de calculer nbPts, le nombre total de points par individu. Pour les caisses de base, pour lesquelles les dispositifs de points gratuits sont intégrés aux points cotisés (étape 3.16), nbPts=nbPtCotise. Pour les caisses complémentaires, on somme les points cotisés et les points gratuits, nbPt=nbPtCotise+nbPtGratuit.
3.17.1 Résultats
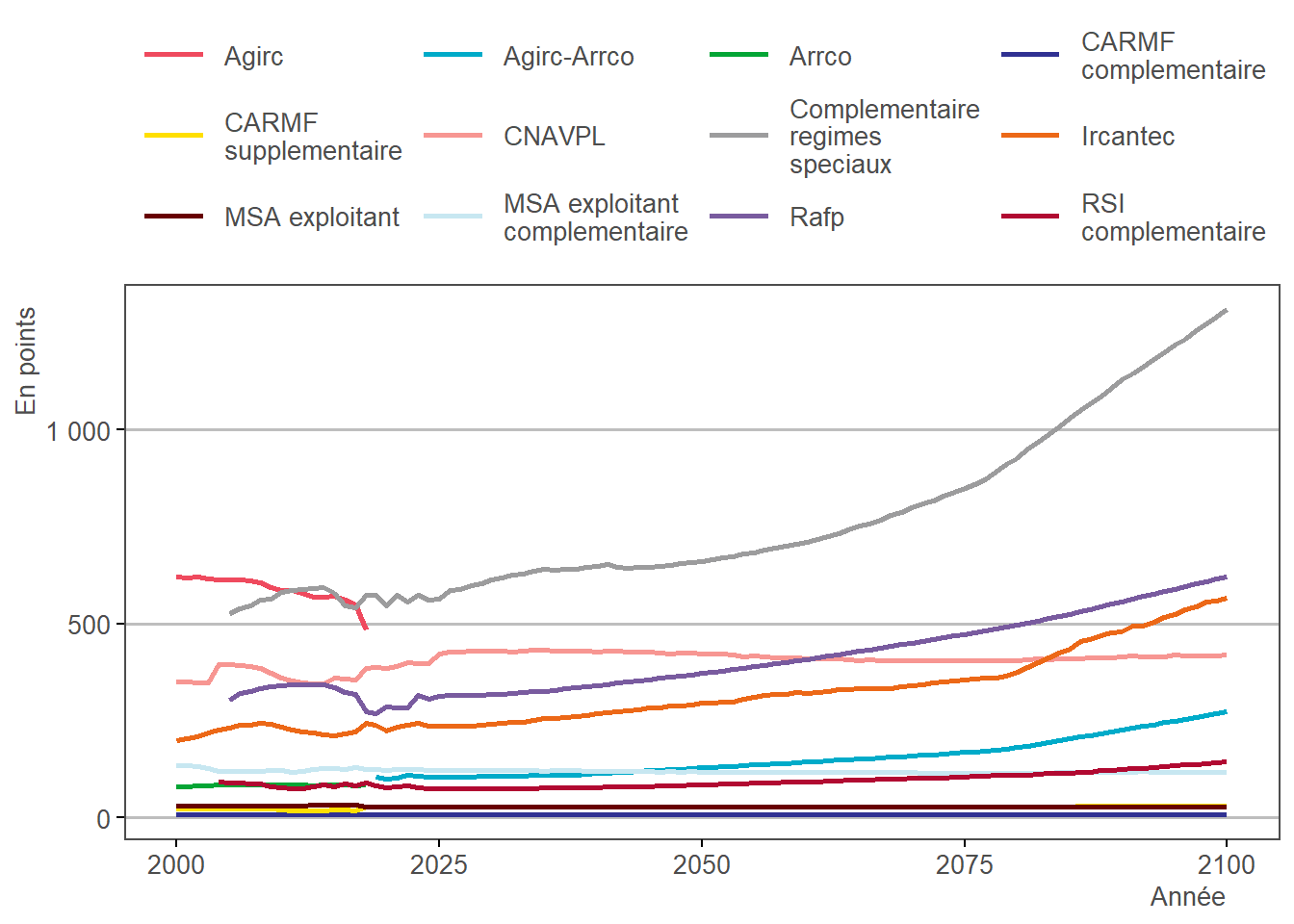
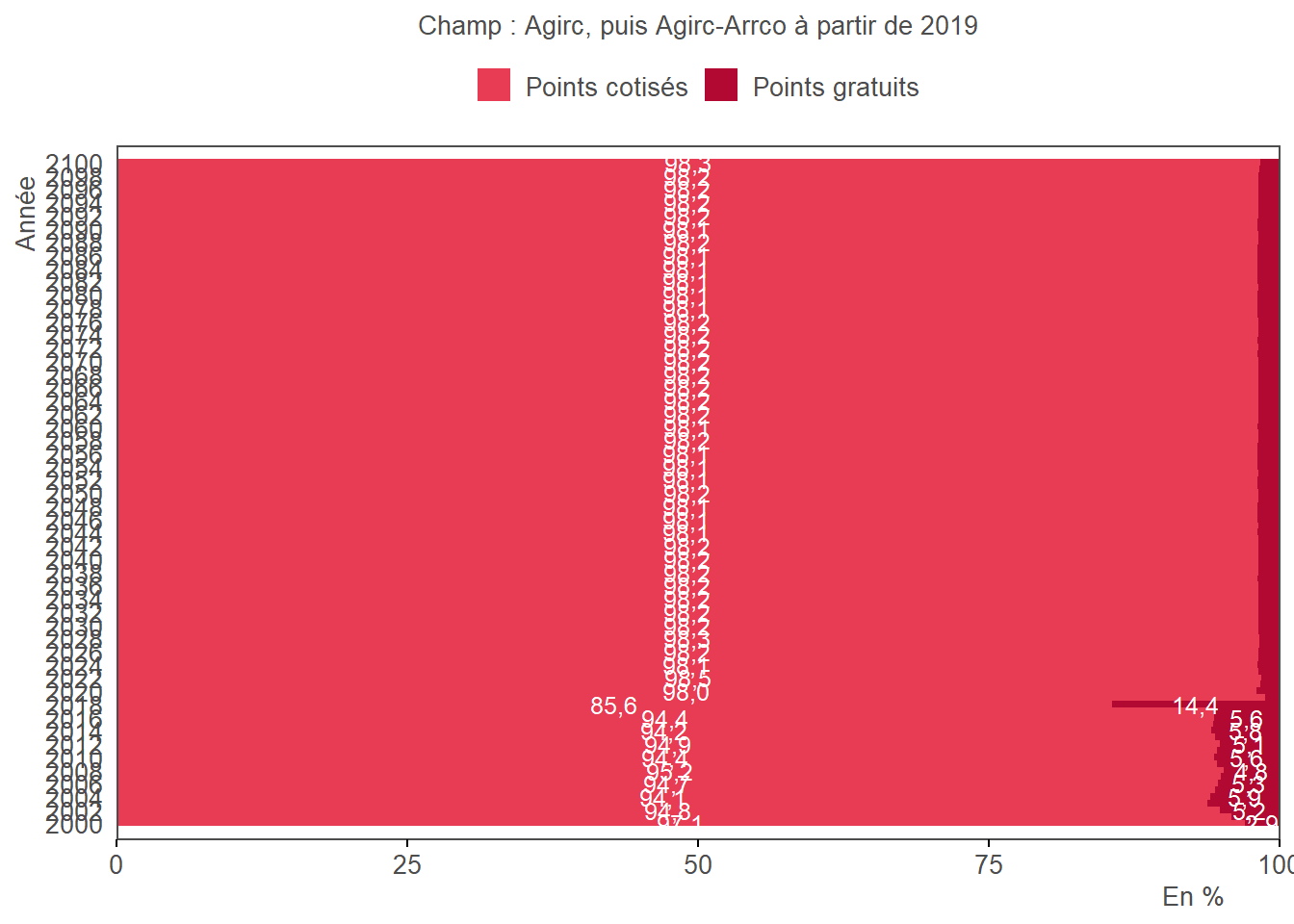
La fusion entre l’Agirc et l’Arrco est à nouveau visible ci-dessus, avec la baisse de la proportion de points gratuits dans le nombre de points total à partir de 2019.
3.18 Calcul des trimestres de majoration de durée d’assurance (MDA) pour enfants
3.18.1 Les règles applicables
La plupart des régimes prévoient l’attribution de trimestres bonus pour les parents, dans des modalités diverses qui ont évolué au cours du temps. Ces trimestres ne sont pas positionnés dans la carrière des individus et sont calculés rétrospectivement au moment de la liquidation. (À cette étape, on ne connaît pas encore la date de liquidation ; aussi Trajectoire suppose que la fin de carrière est relativement stable.) Les régimes complémentaires (RAFP, Agirc-Arco, Ircantec, RCI, régimes complémentaires à la CNAVPL) ne sont pas concernées, non plus que les régimes de bases aux mines (CANSSM) ou à la marine (ENIM).
Dans Trajectoire, l’attribution se fait selon le tableau suivant :
| Régime | Compensation | Détail |
|---|---|---|
| Cnav, régimes alignés et CAVIMAC (cultes) | 8 trimestres | Congés parental en sus |
| CNAVPL (libéraux) et CNBF (avocats) | 8 trimestres | |
| MSA exploitant | 8 trimestres | Congés parental en sus |
| SRE et CNRACL | Jusqu’au 31/12/2003: 4 trimestres en cas d’interruption À partir du 01/01/2004 2 trimestres |
Congés parental en sus ; les trimestres ne comptent pas pour la pro-ratisation (seulement pour le calcul de la décote/surcote) |
| SNCF | 2 trimestres | |
| RATP | Jusqu’au 31/06/2008: 4 trimestres À partir du 01/07/2008: 2 trimestres pour le premier enfant, 4 pour les suivants |
|
| IEG | Jusqu’au 31/06/2008: 0 trimestres À partir du 01/07/2008: 2 trimestres pour le premier enfant, 4 pour les suivants |
Bonifications en cas d’interruption ou réduction du temps de travail en sus |
| Banque de France | Jusqu’au 31/03/2007: À partir du 01/04/2007: 2 trimestres |
|
| CRPCEN (employés de notaires) | Jusqu’au 31/06/2006: 0 trimestres À partir du 01/07/2006: 2 trimestres pour le premier enfant, 4 pour les suivants |
Bonifications en cas d’interruption ou réduction du temps de travail en sus |
Dans la législation, les majorations de durée d’assurance concernent également souvent les adoptions d’enfants mineurs ou la charge d’enfants handicapés voire parfois d’adultes handicapés. Des distinctions sont faites entre les congés “pour accouchement”, réservés à la mère, et les congés “pour éducation”, partiellement partageable entre les parents1. La distinction permet également d’attribuer des majorations y compris pour les fausses couches. Certaines compensations sont conditionnées au fait d’interrompre ou de diminuer l’activité. Ces dispositions ne sont pas implémentées dans Trajectoire.
Les choses se compliquent pour les personnes affiliées à plusieurs régimes, donnant lieu à des règles de compétence d’attribution des majorations pour enfant :
Le régime général est compétent […] lorsque l’assuré a été affilié au régime général et à l’un des régimes suivants : régime des salariés agricoles, régime des non salariés agricoles, ex-régime social des indépendants, régime des professions libérales (dont avocats) et régime des cultes. Si l’assuré a été affilié à deux ou plusieurs des régimes mentionnés précédemment, les majorations de durée d’assurance sont accordées par le régime auquel l’assuré a été affilié en dernier lieu. Lorsque l’assuré a été affilié successivement au régime général et à un régime spécial, le régime spécial est compétent pour attribuer prioritairement une majoration de durée d’assurance liée aux enfants. (…) Toutefois, le régime spécial perd sa compétence dans quatre cas distincts :
- lorsque le régime spécial ne prévoit pas d’avantages familiaux au titre des enfants ;
- lorsque l’assuré n’ouvre pas droit à un avantage familial relatif aux enfants à ce régime spécial ;
- lorsque le régime spécial n’est pas susceptible d’attribuer une retraite en vertu de ses propres règles ;
- lorsque la pension statutaire est attribuée avant la naissance de l’enfant ou la mise en place de l’avantage familial dans ce régime.
Ces règles sont actuellement pas appliquées dans Trajectoire, enfant par enfant. Dans les rares cas où un enfant ne donne pas droit à une majoration, si la personne a un second régime, alors ce régime est sollicité. Nous ne rentrons pas dans le détail de savoir si la personne a suffisamment cotisé pour avoir des droits ouverts dans ce régime.
Pour plus d’informations voir Séance plénière du 19 octobre 2023, COR, Document 2, « Les dispositifs réglementaires de droits familiaux ».
3.18.2 Validité des hypothèses
Les majorations sont distribuées “en bloc”, par exemple 8 au régime général et 4 à la fonction publique (jusqu’en 2003).
Les hommes sont négligeables dans l’attribution des majorations.

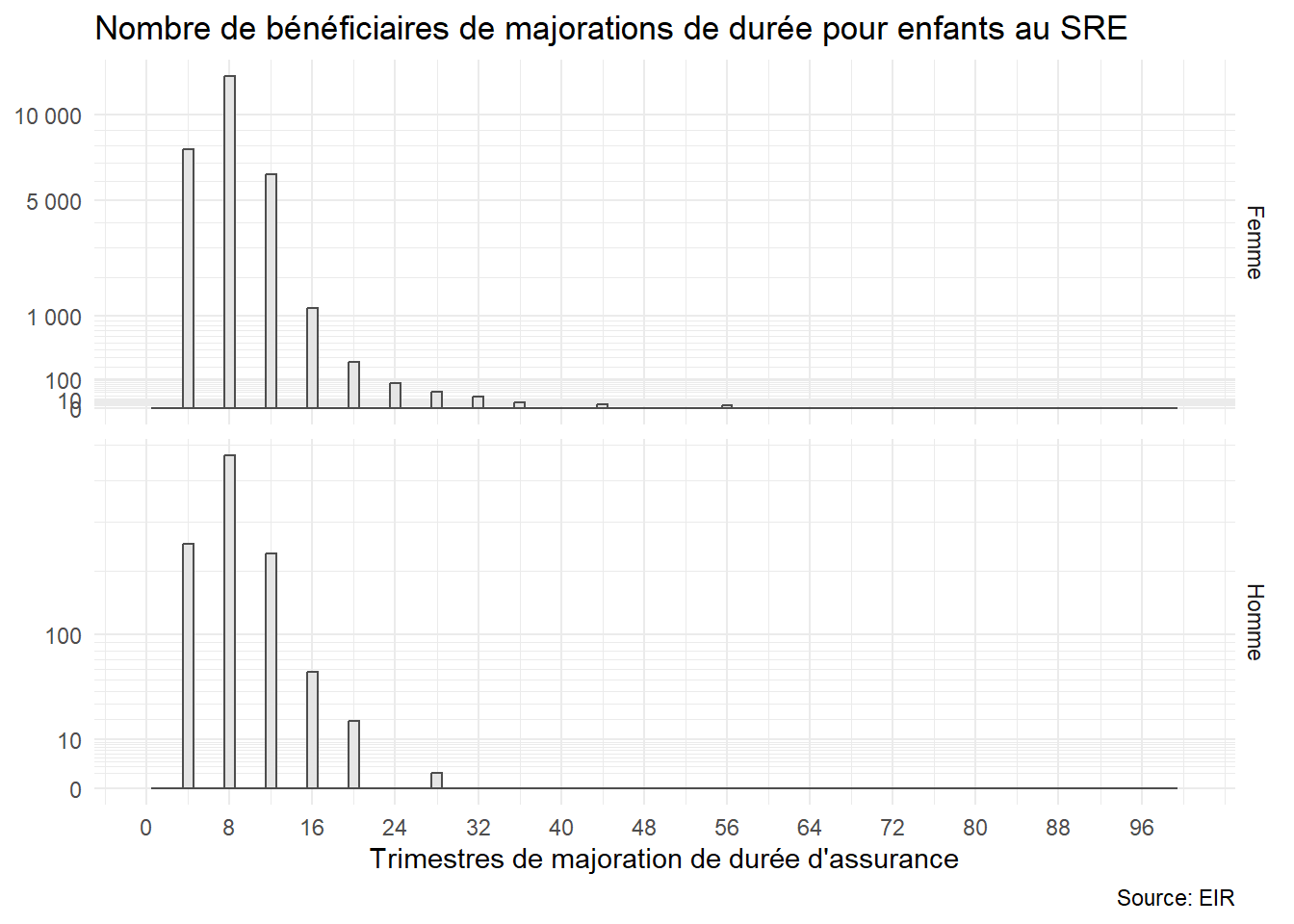
Pas d’évolution récente en faveur des hommes.
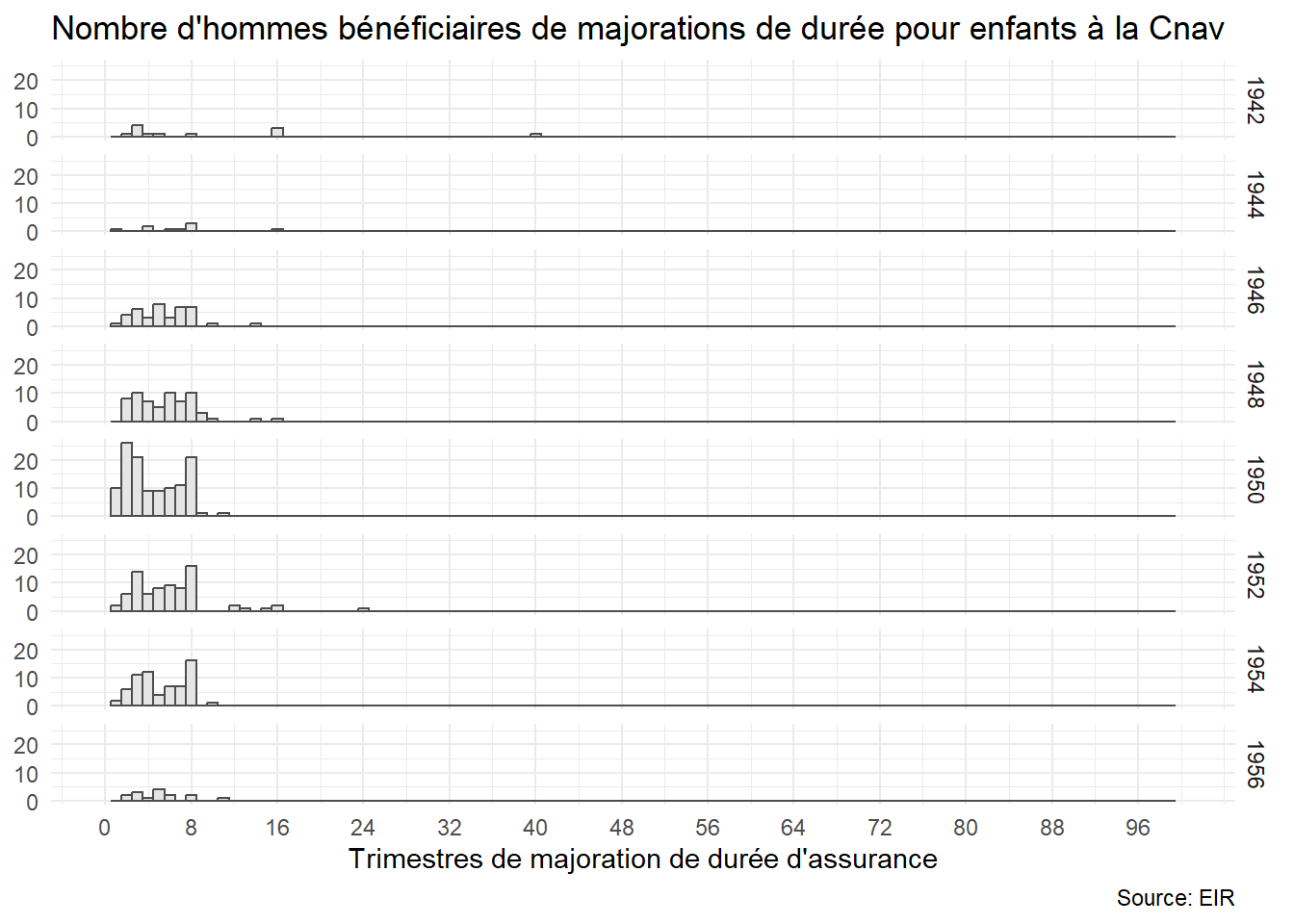
Est-ce que tous les enfants bénéficient de MDA dans la plupart des caisses? On ne peut pas vérifier le lien enfant <-> MDA avec l’EIR seul car on n’a pas directement l’information sur les enfants non impactant la retraite.
Les caisses compétentes pour les majorations de durée ne suivent pas la même répartition que les caisses à cause des poly-affiliés. Ici, les données ne reflètent pas exactement la législation : la préséance des régimes spéciaux et de la fonction publique n’apparaît pas clairement, ni la préséance du régime général sur les autres régimes du privé.
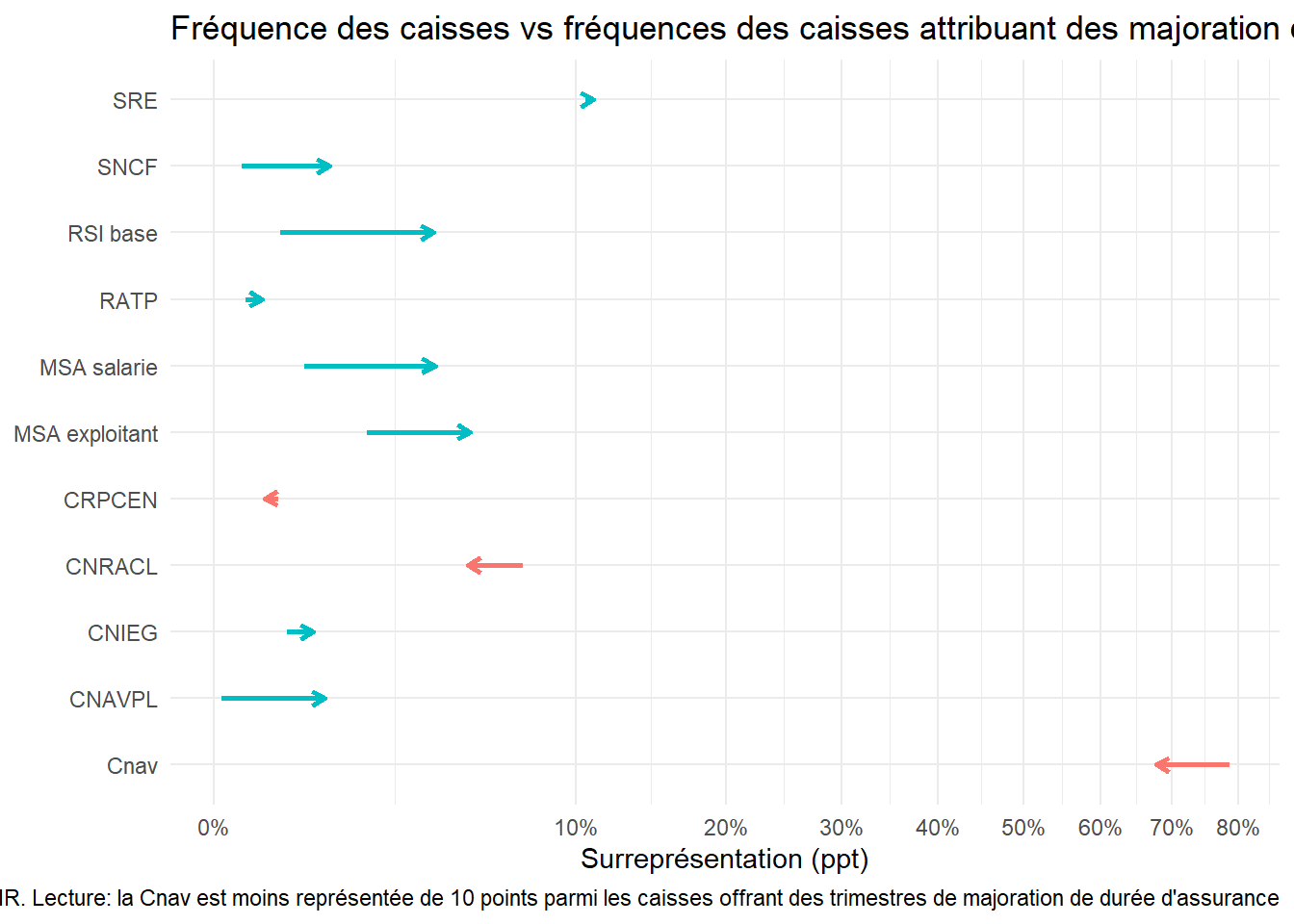
Dernière chose à vérifier, l’hypothèse de stabilité des carrières en fin de carrière. Entre 55 et 60 ans, 96% des personnes encore en activité dans l’EIC gardent la même caisse.
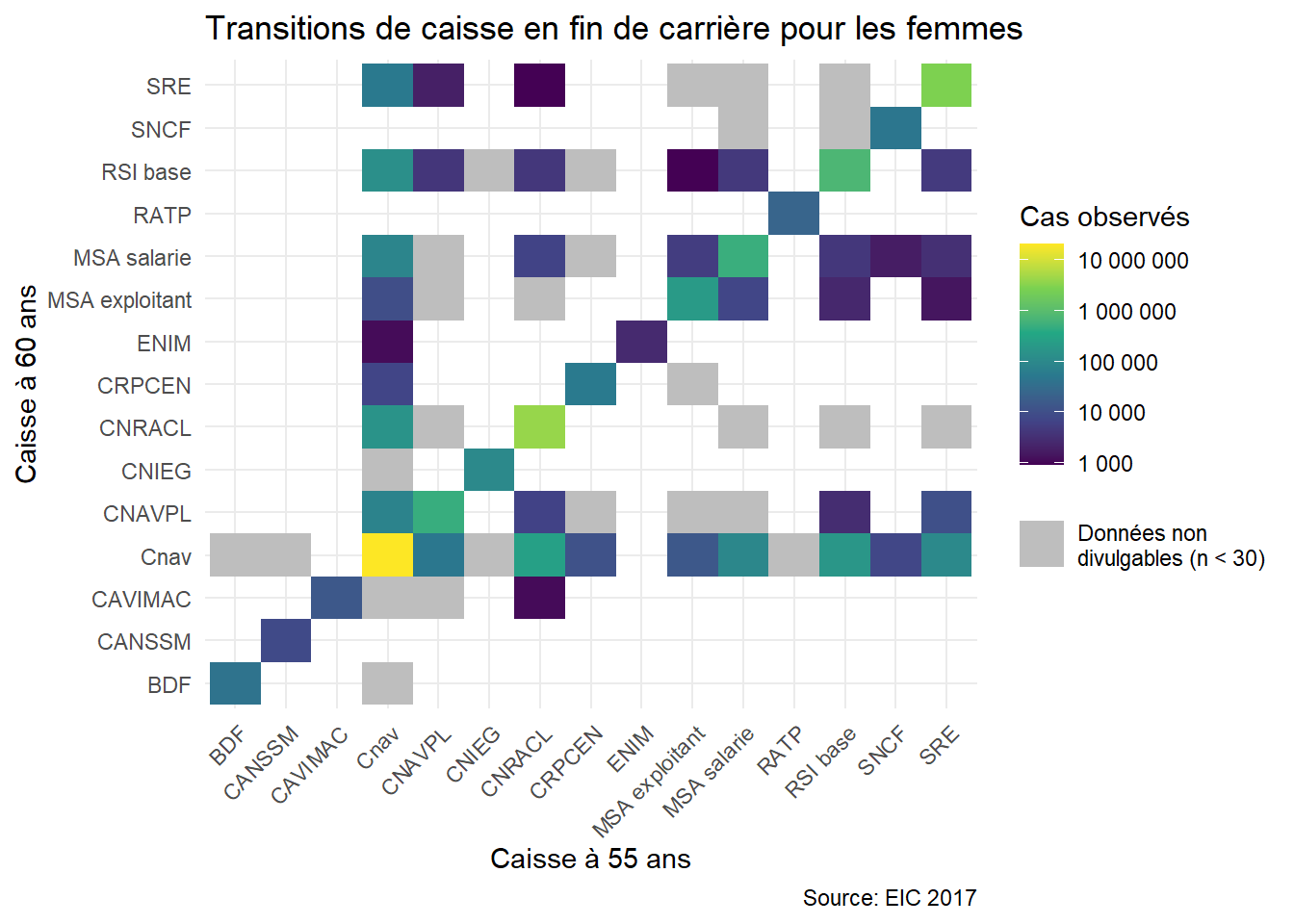
3.18.3 Reproduction dans Trajectoire
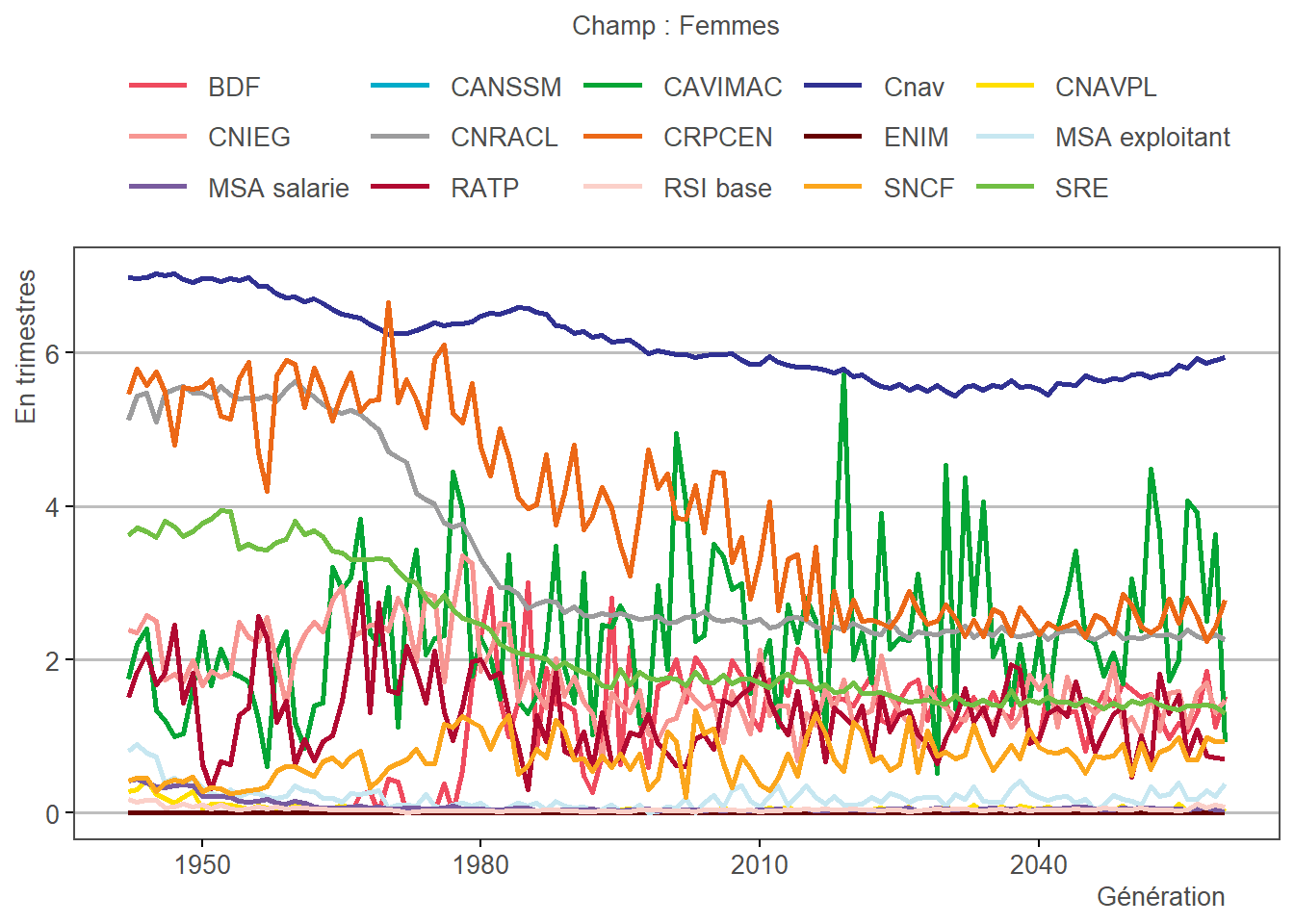
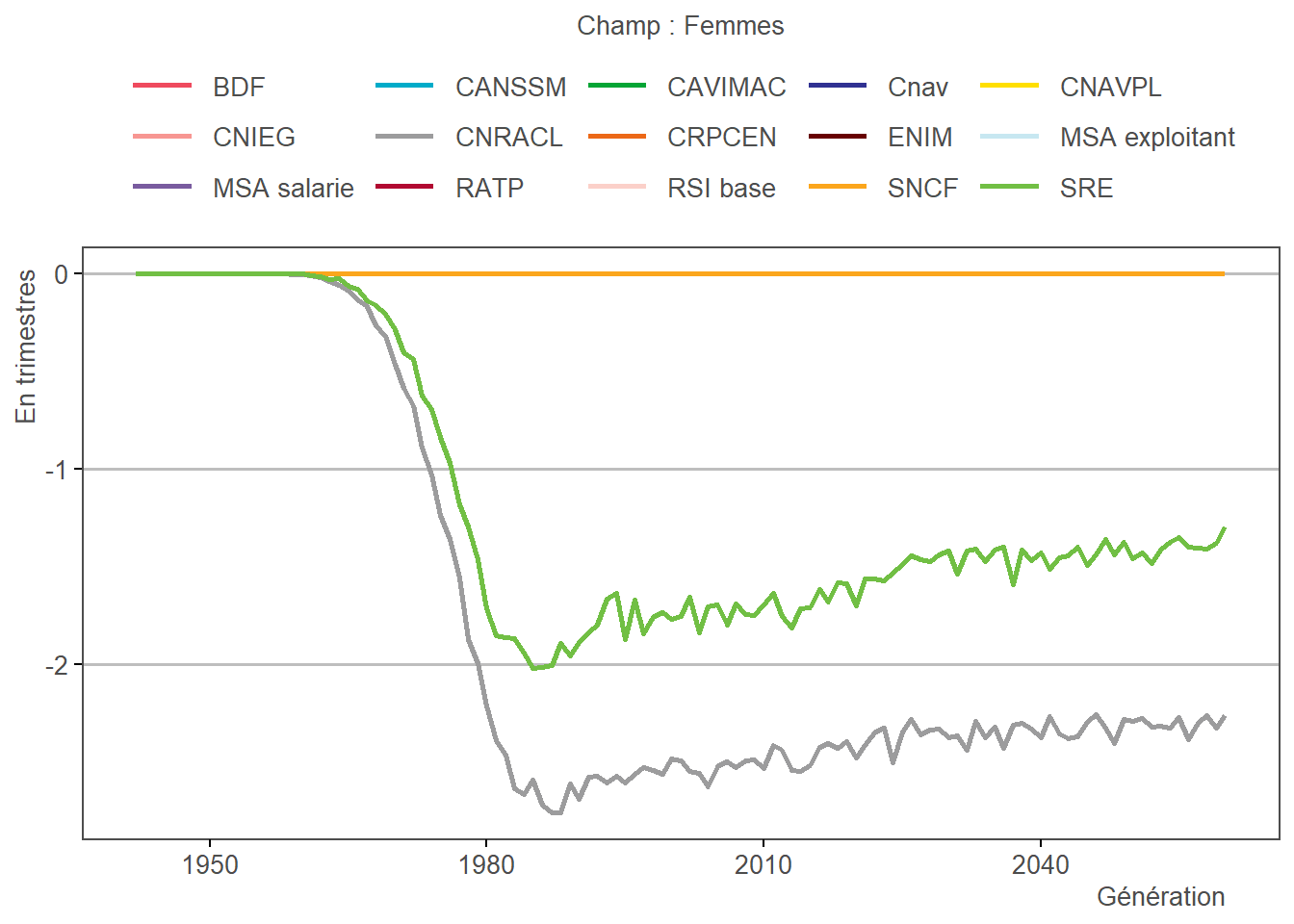
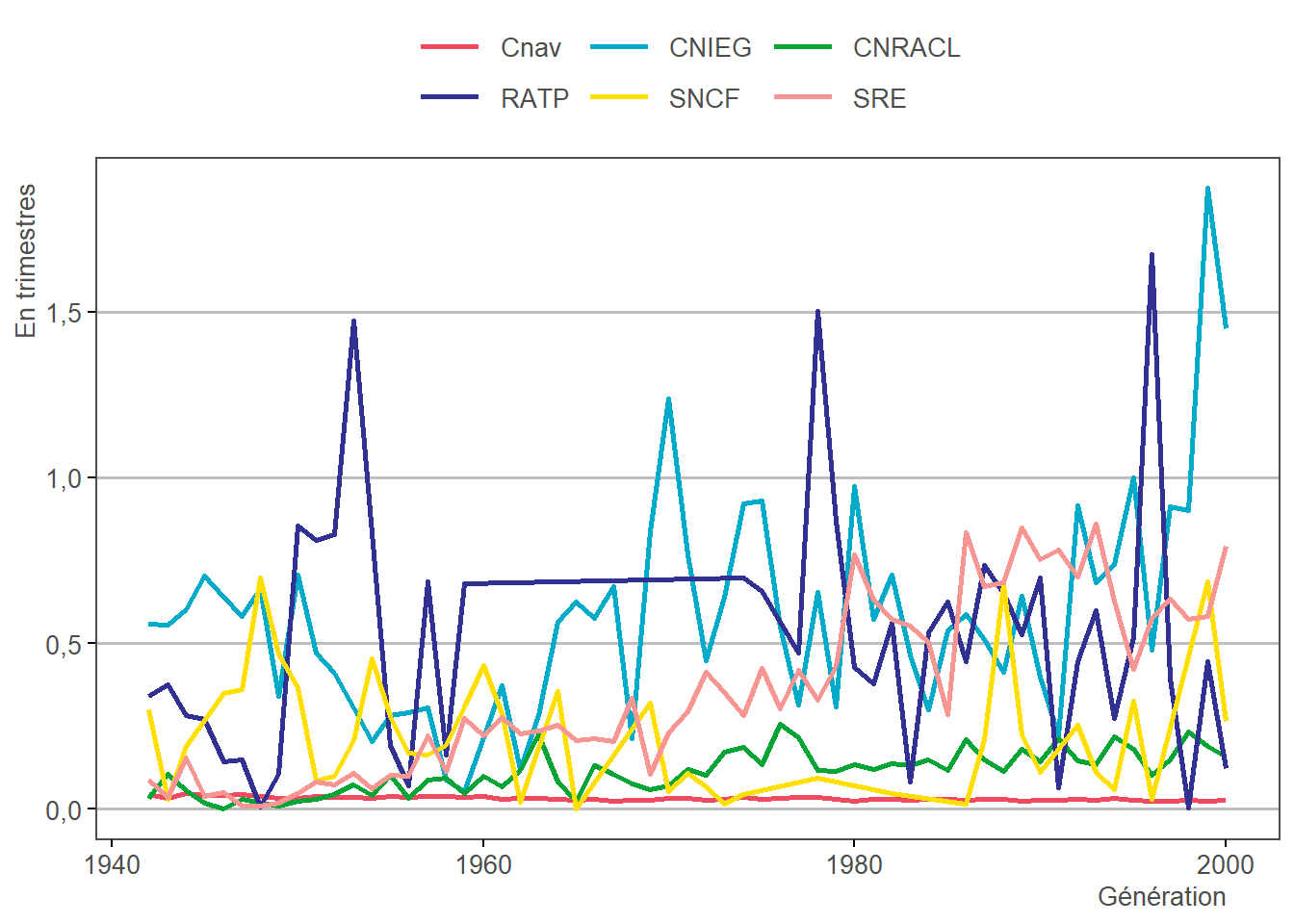
3.19 Imputation des trimestres de bonification
Description : l’étape 3.19 permet d’imputer un nombre de trimestres de bonification attribués aux fonctionnaires, à partir des distributions calculées à l’étape 1.22 :
3.20 Imputation du nombre de trimestres à l’étranger
3.20.1 Description
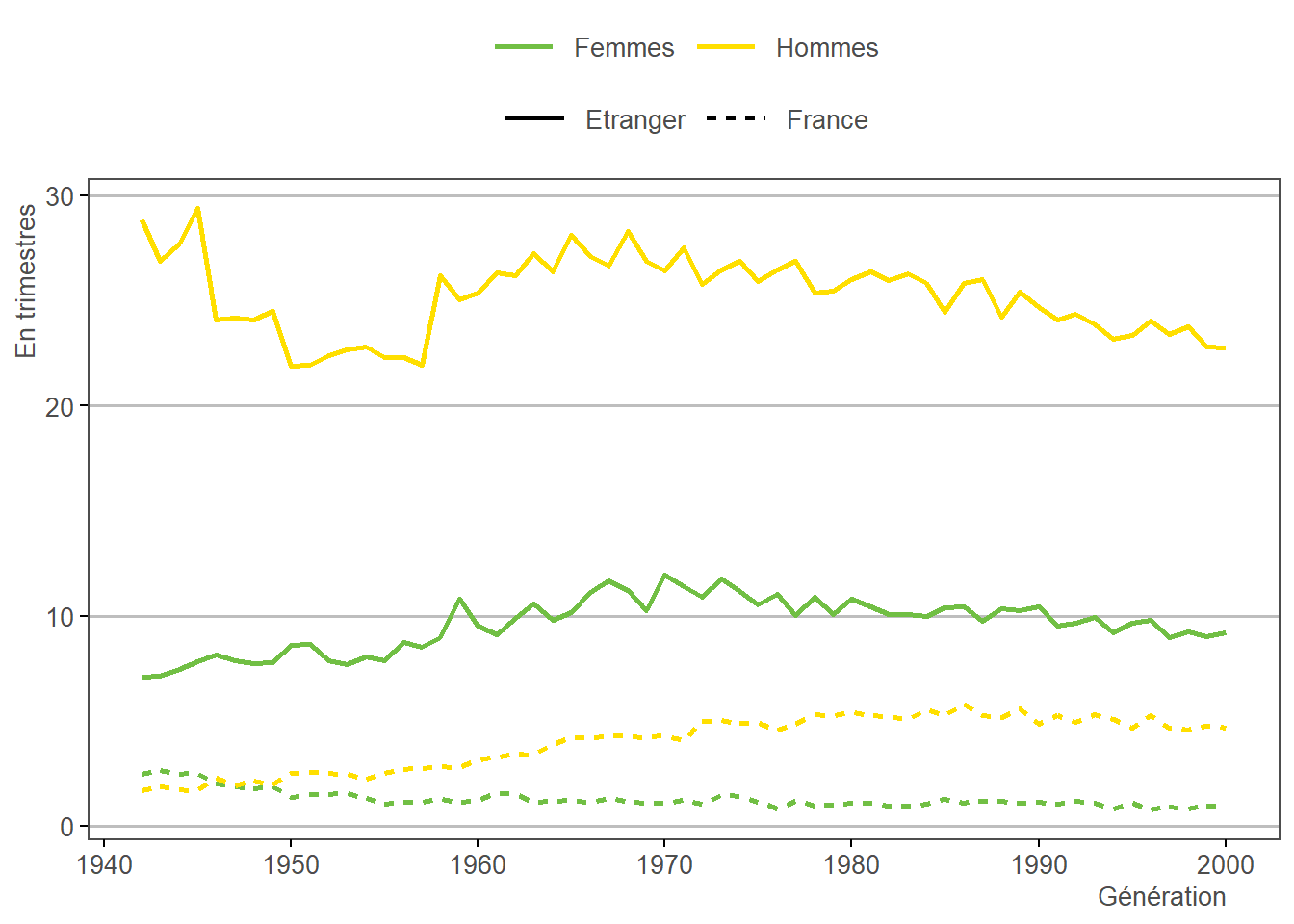
L’étape 3.20 permet d’imputer un nombre de trimestres validés à l’étranger, à partir des distributions calculées à l’étape 1.22. Pour rappel, la distribution du nombre de trimestres à l’étranger est décomposée par sexe, pays de naissance et durée validée tous régimes (divisée en 18 catégories).
Ces trimestres compteront pour la durée validée totale mais pas pour la proratisation. La pension de retraite sera versée par chacun des régimes nationaux, au prorata du temps passé dans chaque pays.
3.20.2 Résultats
3.21 Somme des trimestres additionnels
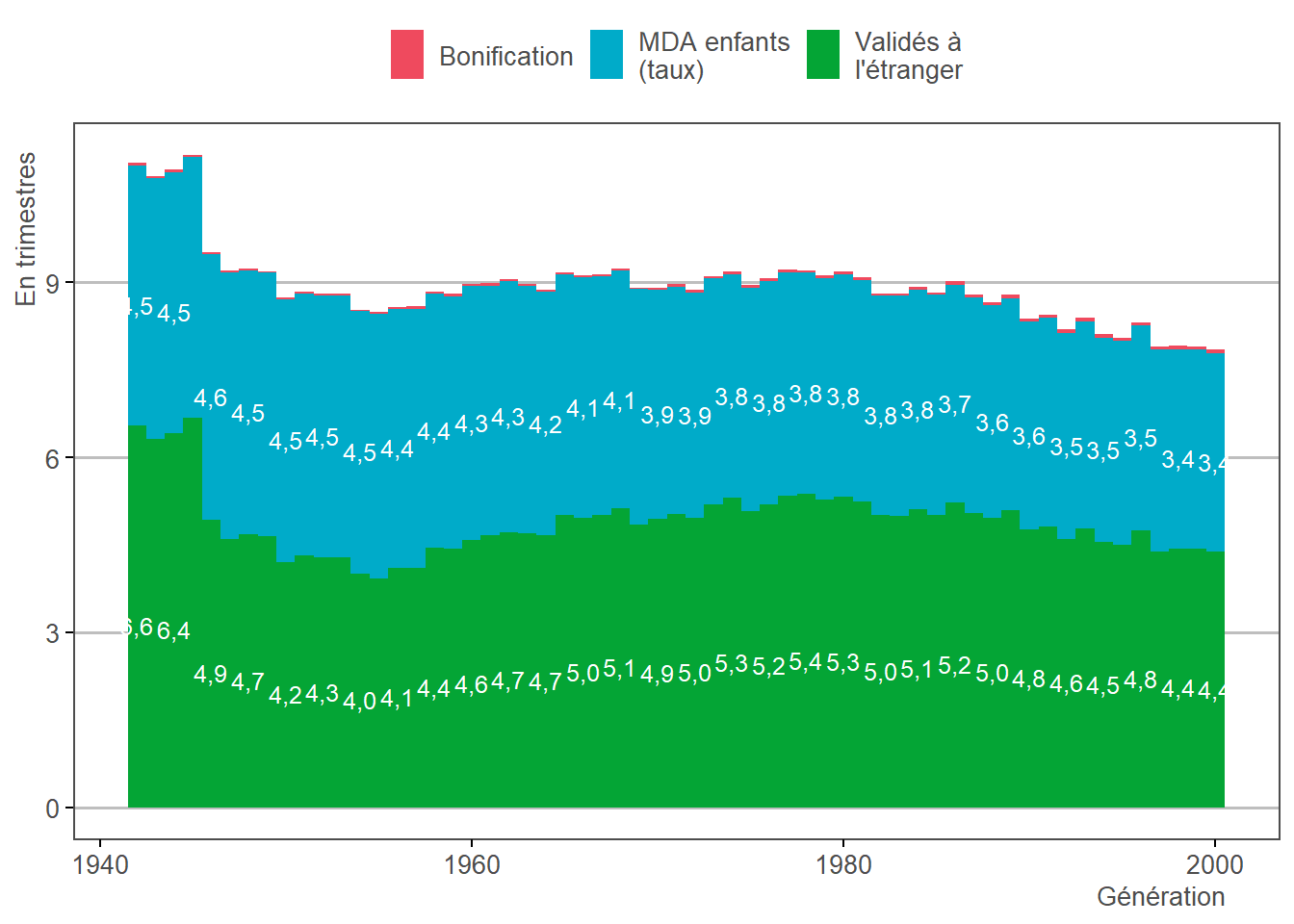
3.21.1 Description
L’étape 3.21 permet de calculer le nombre total de trimestres additionnels pour le taux, selon la formule suivante :
\[\begin{array}{l} nbTrimAdditionnels_i^{taux} = \\ \qquad \begin{array}{l} \sum_{caisses} &nbTrimBonif_i + nbTrimMDAEnfants_i^{taux} + nbTrimEtranger_i \end{array}\end{array}\]
3.21.2 Résultats
3.22 Tirage de l’âge d’inaptitude
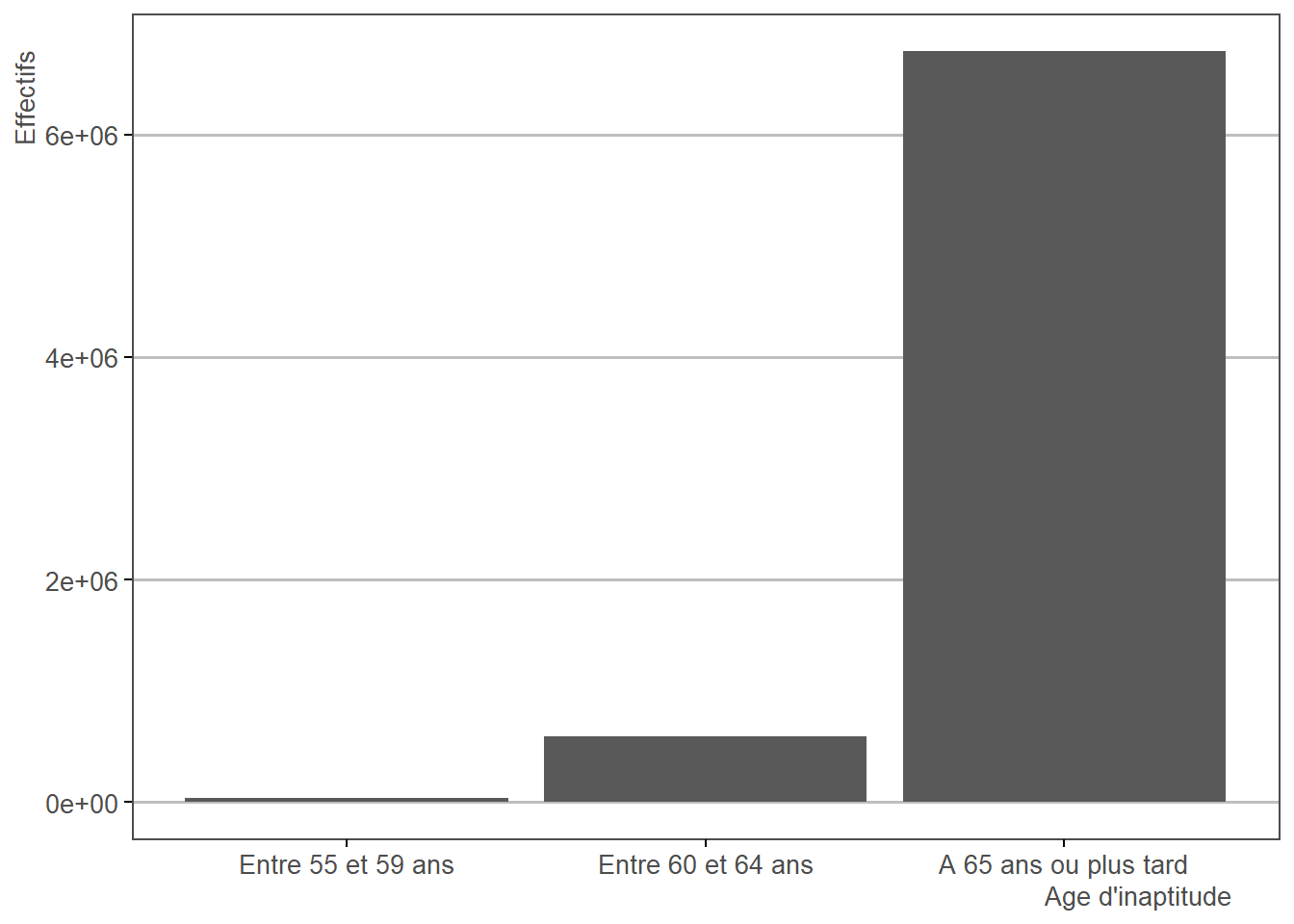
3.22.1 Description
Chaque individu se voit attribuer un âge à partir duquel il ne peut plus travailler. Après cet âge, il liquidera en inaptitude et bénéficira de droits à la retraite particuliers.
Pour imputer cet âge d’inaptitude, on utilise le modèle de survie estimé à l’étape 1.27. Les caractéristiques de l’individu (sexe, caisse et nombre de trimestres cotisés entre 50 et 55 ans), ainsi que son aléa d’inaptitude, vont permettre de déterminer le temps de “survie” après 49 ans, et donc l’âge d’inaptitude.
3.22.2 Résultats
3.23 Calcul trimestres pour proratisation fonctionnaires
Contrairement à la durée validée comptant pour le calcul du taux, la durée validée comptant pour la proratisation (ou durée de services) dépend de la quotité de travail du fonctionnaire. Pour rappel, l’imputation des temps partiels, et donc de la quotité, est effectuée à l’étape 2.30.
La formule de calcul est donc la suivante :
\[nbTrimValidePourDureeService = nbTrimValide * quotite/100\] A noter : par défaut, la durée de services dans les régimes spéciaux reste fixée à 4 trimestres annuels.
3.24 Bonif et MDA déterministes pour fonctionnaires
C’est une étape spécifique au calcul des cas types. La bonification de trimestres correspondante au cas type en question est imputée ici directement.
« À la suite des arrêts rendus par la Cour de justice de l’Union européenne et par la Cour de cassation, le droit français a été modifié et a ouvert les dispositifs de majoration de durée d’assurance au bénéfice des hommes en 2003 dans les régimes de la fonction publique, en 2008 dans les autres régimes spéciaux et en 2010 au régime général. »↩︎