$hypSmpt
[1] 1
$scenarioMortalite
[1] "central"
$hypFecondite
[1] "central"
$hypImmigration
[1] "Centrale"
$hypChomage
[1] "Var4,5%_avant_réf"
$mortaDiff
[1] TRUE
$lura
[1] TRUE
$indCorrectionRemuSexe
[1] FALSE
$remuNulleHorsEqua
[1] TRUE
$methodeEquaSal
[1] "salaireSansEqua"
$anneeMinEqua
[1] 1988
$effetHorizon
[1] FALSE
$blocageTransitionFinDeVie
[1] TRUE
$tirageCategFoncParEligibilite
[1] FALSE
$correctionTransitionApres60
[1] TRUE
$ageMaxTransition
[1] 57
$decoteQueSurAge
[1] FALSE
$fonctionnaireAuTP
[1] TRUE
$fichierCorCotisant
2023 2024
"hypo_cotisants_chômage_2023.xlsx" "hypo_cotisants_chômage_2024.xlsx"
$fichierCorSalairePrix
2023 2024
"hypo_Salaires_Prix_PIB_V4.xlsx" "hypo_Salaires_Prix_PIB_2024.xlsx"
$fichierCorParametres
2023 2024
"hypo_parametres_2023_V2.xlsx" "hypo_paramètres_2024.xlsx"
$fichierCorTauxCotis
[1] "hypo_taux_cotisation_et_legislation_2020_drees.xlsx"
$fichierCorDureeRetraite
[1] "Données_RA2020_P4.xlsx"
$fichierPSTAB
[1] "Synthèse_PSTAB_2022_V6.xlsx"
$genMax
[1] 2060
$genMaxEic
[1] 1994
$genMinEic
[1] 1942
$genFusionEicEir
[1] 1950
$genMin
[1] 1951
$anneeEic
[1] 2017
$anneeEir
[1] 2016
$anneeEuroConstant
[1] 2023
$anneeActuelle
[1] 2024
$anneeProjection
[1] 2100
$anneeMaxEacr
[1] 2020
$ageMax
[1] 70
$graine
[1] 1
$maxIntAlea
[1] 2000000000
$ageMortMax
[1] 110
$verboseCharge
[1] TRUE
$anneeMinGraphes
[1] 2010
$anneeMaxGraphes
[1] 2060
$genMinGraphes
[1] 1950
$genMaxGraphes
[1] 2000
$anneeMinAttritionFaible
[1] 2018
$genMinAttritionFaible
[1] 1955
$indFonctionLancerModeleEnCours
[1] FALSE
$listeAn
[1] 2016 2017 2018 2019 2020 2021 2022 2023 2024 2025 2026 2027 2028 2029 2030
[16] 2031 2032 2033 2034 2035 2036 2037 2038 2039 2040 2041 2042 2043 2044 2045
[31] 2046 2047 2048 2049 2050 2051 2052 2053 2054 2055 2056 2057 2058 2059 2060
[46] 2061 2062 2063 2064 2065 2066
$listeRegimesSpeciaux
[1] "SNCF" "ENIM" "CANSSM" "CAVIMAC" "CNIEG" "RATP" "CRPCEN"
[8] "BDF"
$listeCaissesBase
[1] "BDF" "CANSSM" "CAVIMAC" "Cnav"
[5] "CNAVPL" "CNIEG" "CNRACL" "CRPCEN"
[9] "ENIM" "MSA exploitant" "MSA salarie" "RATP"
[13] "Regime special" "RSI base" "SNCF" "SRE"
$listeCaissesFonc
[1] "BDF" "CANSSM" "CAVIMAC" "CNIEG"
[5] "CNRACL" "CRPCEN" "ENIM" "RATP"
[9] "Regime special" "SNCF" "SRE"
$listeCaissesComp
[1] "Agirc" "Agirc-Arrco"
[3] "Arrco" "CARMF complementaire"
[5] "CARMF supplementaire" "Complementaire regimes speciaux"
[7] "Ircantec" "MSA exploitant complementaire"
[9] "Rafp" "RSI complementaire"
$listeCaissesRegimesAlignes
[1] "Cnav" "MSA salarie" "RSI base"
$listeEtats
[1] "Salarie du prive non cadre" "Salarie du prive cadre"
[3] "Contractuel de la FP" "Independant"
[5] "SNCF" "ENIM"
[7] "CANSSM" "CAVIMAC"
[9] "CNIEG" "RATP"
[11] "CRPCEN" "BDF"
[13] "Regime special avec statut Cnav" "Sans etat secondaire"
[15] "AVPF" "Inactif"
[17] "Chomage" "Maladie"
[19] "Invalidite" "FPE"
[21] "FPT ou FPH" "Exploitant agricole"
[23] "MSA salarie" "Liberal"
[25] "Regime special" "Inactif ou retraite"
[27] "Retraite" "FPE temps partiel"
[29] "FPT ou FPH temps partiel"
$listeRegimesEquilibres
[1] "SRE" "Regimes speciaux"
[3] "Regime special" "SNCF"
[5] "ENIM" "CANSSM"
[7] "CAVIMAC" "RATP"
[9] "CRPCEN" "BDF"
[11] "Complementaire regimes speciaux" "Rafp"
$rendementNouveau
[1] 5.52 Importations
2.1 Définition des paramètres Trajectoire
Les paramètres Trajectoire caractérisent une simulation donnée. Ils peuvent être modifiés par la suite pour générer des variantes. Par exemple, la simulation de référence, ou scénario central, est définie par les paramètres suivants.
2.2 Téléchargement des ‘barêmes IPP’
Téléchargement des “barêmes IPP” de l’Institut des Politiques Publiques (IPP), une base de données historique sur l’état de la réglementation socio-fiscale. Ces “barèmes” sont utilisés notamment pour suivre la réglementation en vigueur dans les différentes caisses de retraites non directement gérées par l’État.
Cette étape est sautée sur le CASD, qui ne possède pas d’accès à Internet. Les données les plus récentes sont régulièrement mises en cache à l’intérieur du package.
2.3 Lecture des “barèmes IPP”
Lecture des sous-dossiers d’intérêt parmi les données téléchargées, dans un format brut.
2.4 Mise en forme des “barêmes IPP”
“Mise à plat” des structures de données imbriquées obtenues à la étape 2.3.
2.5 Téléchargement des données du Panorama 2021 de la DREES
Importation d’une partie des tableaux de données de l’édition 2021 de la collection “Panorama” Les retraités et les retraites de la Direction de la recherche, de l’évaluation, des études et des statistiques (DREES). Ces données permettent de contextualiser le projections de trajectoire avec des données administratives historiques.
Cette étape est sautée sur le CASD, qui ne possède pas d’accès à Internet. Les données les plus récentes sont régulièrement mises en cache à l’intérieur du package.
2.6 Lecture des données Drees
Lecture et formatage des fichiers précédemment téléchargés.
2.7 Importation des paramètres du Conseil d’Orientation des retraites (COR)
Importation des données fourniers par le Conseil d’Orientation des Retraites (COR), historiques ou prospectives.
Données historiques
Données previsionnelles
2.8 Importation paramètres autres
Importation de fichiers historiques (provenant d’une étude interne) et de fichiers de l’Institut des Politiques publiques (IPP) dont l’automatisation n’a pas encore été proprement recodée.
2.9 Conciliation des “barêmes IPP” et des paramètres Trajectoire
Lorsque deux sources existent pour les mêmes paramètres, par exemple une source de données historiques, et une source de données prospectives, Trajectoire aligne les deux sources de façon la plus judicieuse possible.
2.10 Importation données de l’Insee et de l’Enquête annuelle auprès des caisses de retraite (EACR)
Importation de données de l’Institut national de la statistique et des études économiques (INSEE).
La table dtMortalite possède 115434 lignes et seul un échantillon aléatoire de 100 lignes est présenté ici.
Importation de données issues de l’Enquête annuelle auprès des caisses de retraite (EACR).
La table dtEacrC possède 101084 lignes et seul un échantillon aléatoire de 100 lignes est présenté ici.
2.11 Importation des individus décédés (ou “sortants”) entre l’EIC 2013 et l’EIC 2017
Les personnes présentes dans l’échantillon inter-régime des cotisants (EIC, voir étape 2.13) en 2013 sont normalement suivies de la même façon en 2017. Seulement, il existe des raisons pour lesquelles une personne peut “sortir” entre deux vagues d’enquête, dont la plus probable est le décès. Dans ce cas, Trajectoire utilise les données connues de 2013. Cette étape consiste à importer les informations connues sur les “sortants”, notamment leur date de décès.
2.12 Importation de l’échantillon EIC-Insee
L’Insee sélectionne les personnes présentes dans l’échantillon inter-régime des cotisants (EIC, voir étape 2.13) en 2017, à partir de l’échantillon de 2013. L’échantillon contient l’année de naissance (ou “génération”), le mois de naissance, le genre et le pays de naissance. Lorsqu’une personne préalablement suivie est décédée avant le tirage de l’échantillon, on connaît de plus la date de décès. Si elle décède après le tirage, la date de décès est obtenue au moment de l’enquête (cf. étape 2.11).
2.13 Importation de l’Echantillon inter-régime des cotisants (EIC) 2017 pour les pensions de base
L’Echantillon inter-régime des cotisants (EIC) recense les droits ouverts dans chaque régime de retraites pour un échantillon de la population. Cette section importe uniquement les régimes de pension de base ; la étape 2.14 s’intéresse aux pensions complémentaires. Pour les “sortants” (cf. étape 2.11), Trajectoire complète l’information de l’EIC 2017 par l’EIC 2013.
Trajectoire ne modélise pas les régimes de retraite les plus minoritaires.
2.14 Importation de l’EIC 2017 pour les pensions complémentaires
Importation similaire à la étape 2.13.
Trajectoire ne modélise pas les régimes de retraite complémentaire les plus minoritaires.
2.15 Importation et traitement de l’Echantillon inter-régime des retraités de 2016 (EIR 2016)
L’échantillon inter-régime des retraités (EIR ; étape 3) recense les droits ouverts dans chaque régime de retraites pour un échantillon de personnes à la retraite. Il permet à Trajectoire d’analyser les comportements de personnes ayant achevé leur carrière, notamment pour la modélisation des départs à la retraites (étape 2.24).
L’EIR 2016 est traitée de façon similaire à l’EIC 2017, tel que décrit à la étape 2.13, la étape 2.11 et la étape 2.19.
2.16 Importation et traitement des Déclarations Annuelles de Données Sociales (DADS)
Trajectoire utilise les Déclarations Annuelles de Données Sociales (DADS) pour estimer, par régression linéaire, les primes des fonctionnaires.
2.17 Importation des résultats du Conseil d’orientation des retraites (COR)
Le Conseil d’orientation des retraites (COR) fournit des projections en termes d’effectifs de retraités, et de masses financières (masses de prestations, de cotisations, solde financier du système). Ces projections servent notamment à effectuer des validations externes de Trajectoire.
2.18 Corrections diverses de l’EIC
Différentes corrections sont appliquées :
- Des valeurs manquantes sont mises à zéro.
- On détecte si l’individu a gagné des trimestres ou des points pour cause de maladie ou de chômage.
- Les rémunérations annuelles des individus indiqués comme retraités en fin d’année sont définies comme manquantes car elles sont tronquées sans qu’on sache précisément quand. Sans cette précaution, on sous-estime les rémunérations des supérieurs à 60 ans.
2.19 Simplification des régimes de retraites dans l’EIC
2.19.1 Simplification des régimes de base
Trajectoire modélise 8 caisses de base couvrant l’essentiel de la population : la Caisse nationale d’assurance vieillesse (Cnav), la Sécurité sociale des indépendants (SSI), la Mutualité sociale agricole (MSA) salarié, la MSA exploitant, le Service des retraites de l’État (SRE), la Caisse nationale de retraite des agents des collectivités locales (CNRACL), la Caisse nationale d’assurance vieillesse des professions libérales (CNAVPL) et le régime SNCF. Les autres régimes sont modélisés au plus proche.
Concrètement, cela signifie qu’une personne ayant cotisé la même année dans la fonction publique civile et militaire verra les deux rémunérations agrégées dans une seule catégorie “fonction publique (SRE)”. Les décomptes de trimestres cotisées sont agrégés de la même façon.
Traitement des régimes spéciaux
Les régimes spéciaux (SNCF, RATP, Banque de France, Marine, Mines, Cultes, industries électrique et gazière, clercs et employés de notaires) sont tous modélisés comme la SNCF mais, contrairement aux autres simplifications de modélisation, chaque régime est maintenu formellement distinct. Ce choix permet la simulation de l’extinction de ces régimes prévue à des échéances différentes. Cela signifie également que les rémunérations et les trimestres cotisés dans chaque régime sont maintenus distincts.
Regroupements des caisses de base
| Caisse initiale (code EIC) | Caisse de référence |
|---|---|
| 0010 | Cnav |
| 0021 | MSA salarié |
| 0022 | MSA exploitant |
| 0012, 0013, 0033 | SRE |
| 0032 | CNRACL |
| 0040, 0042, 0050 | SSI |
| 2011, 2021, 2031, 2041, 2051, 2061, 2071, 2081, 2101, 2111, 2121, 2211, 2231 | CNAVPL |
| 0060, 0070, 0080, 0090, 0100, 0300, 0500, | SNCF |
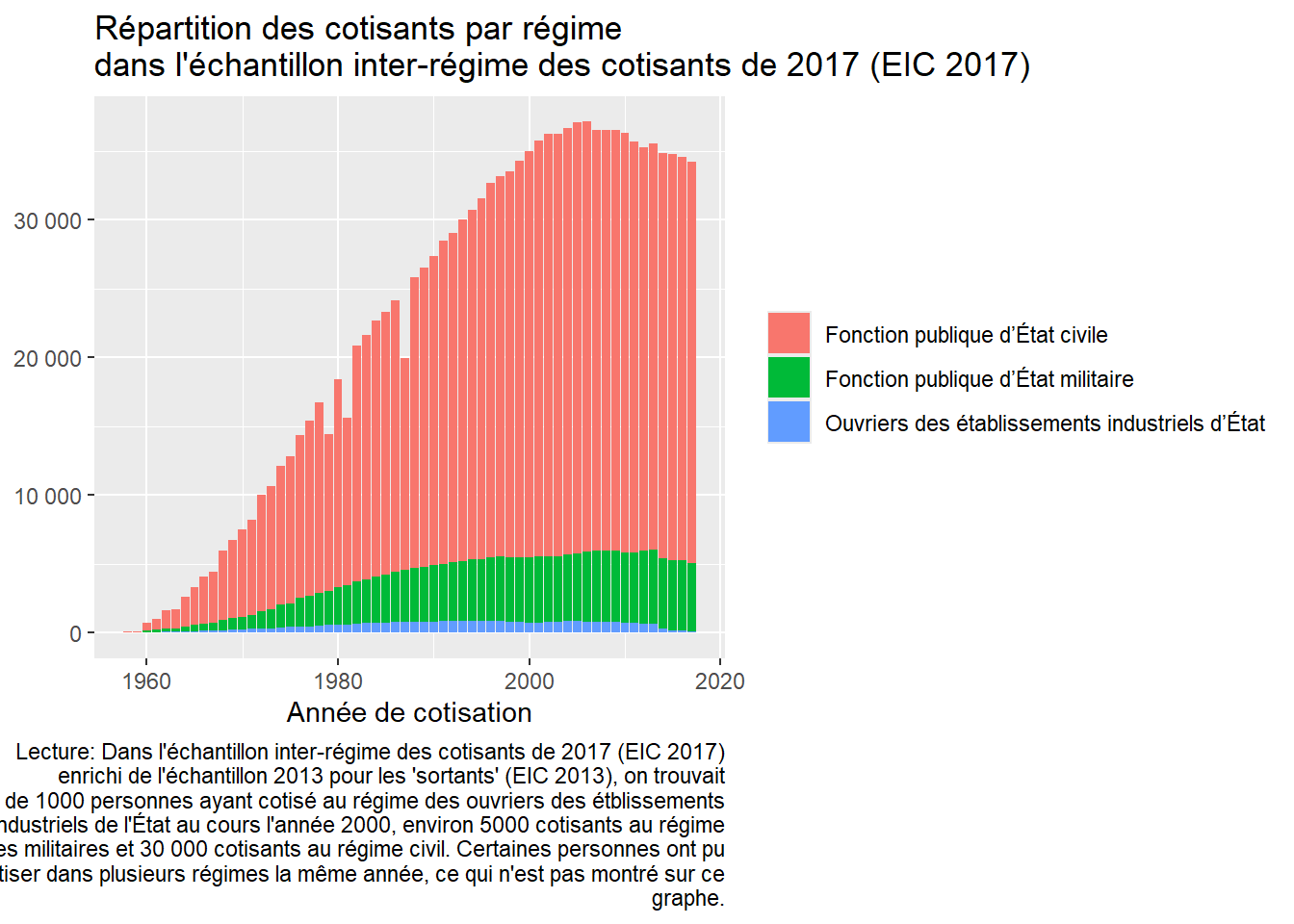
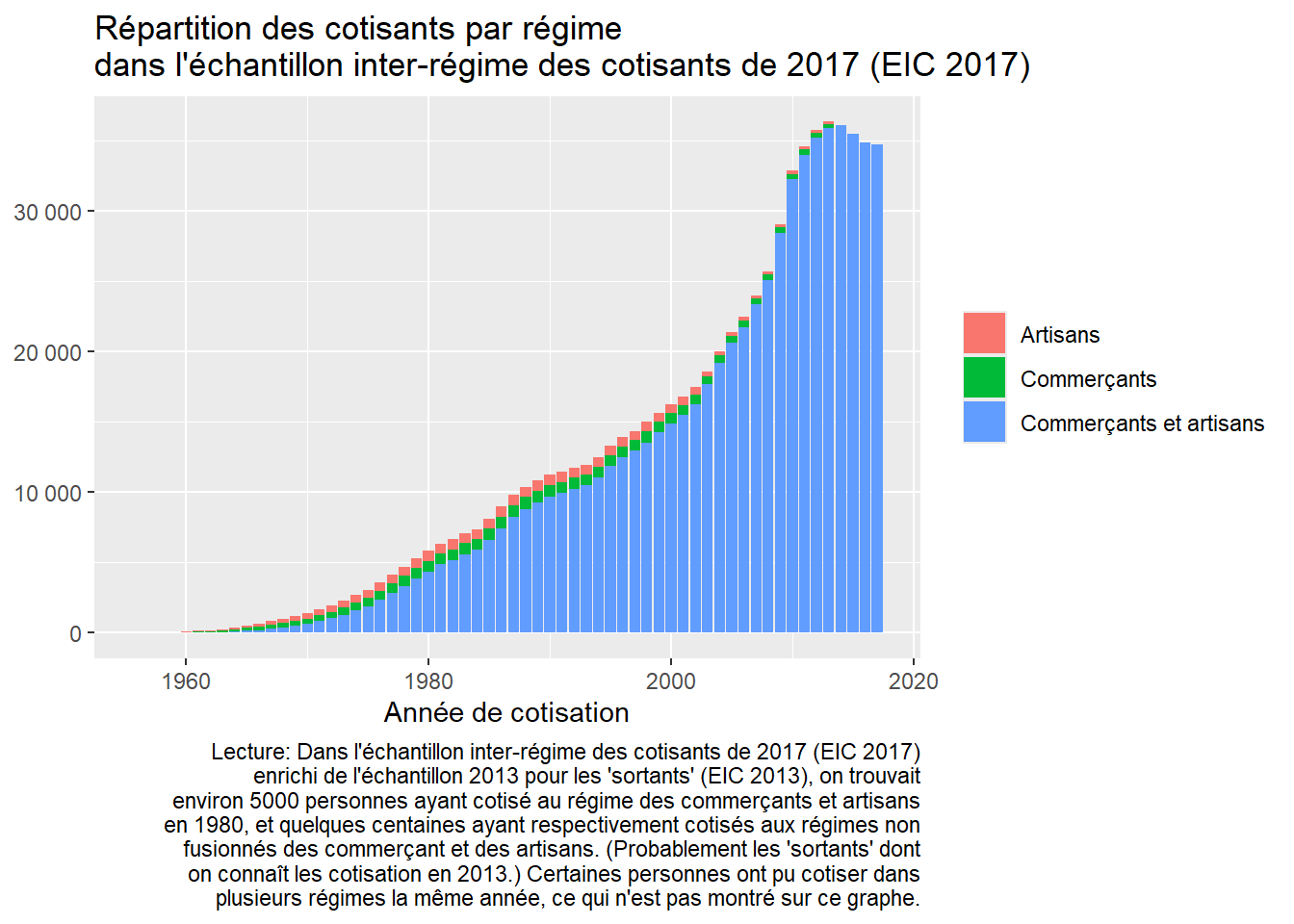
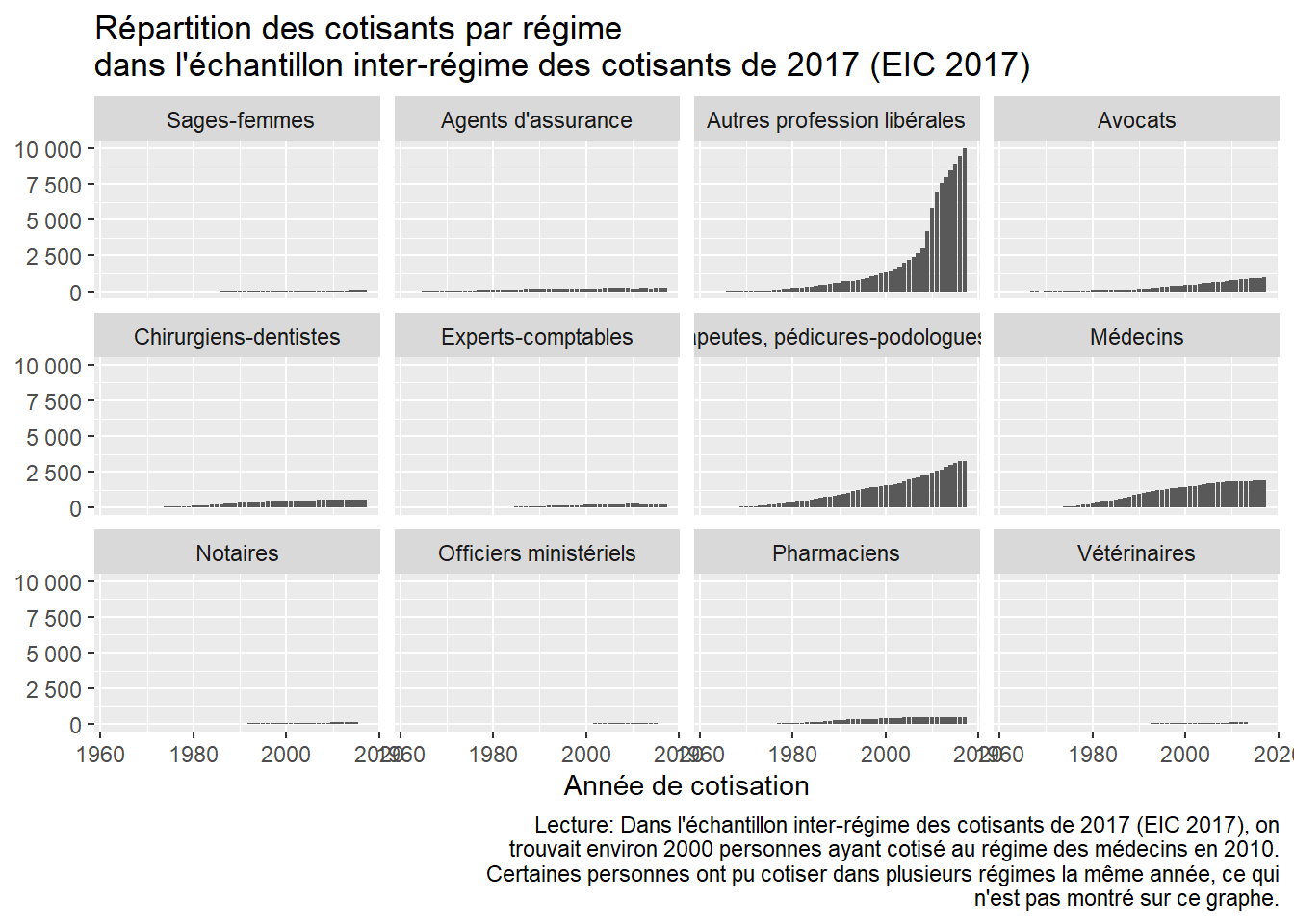
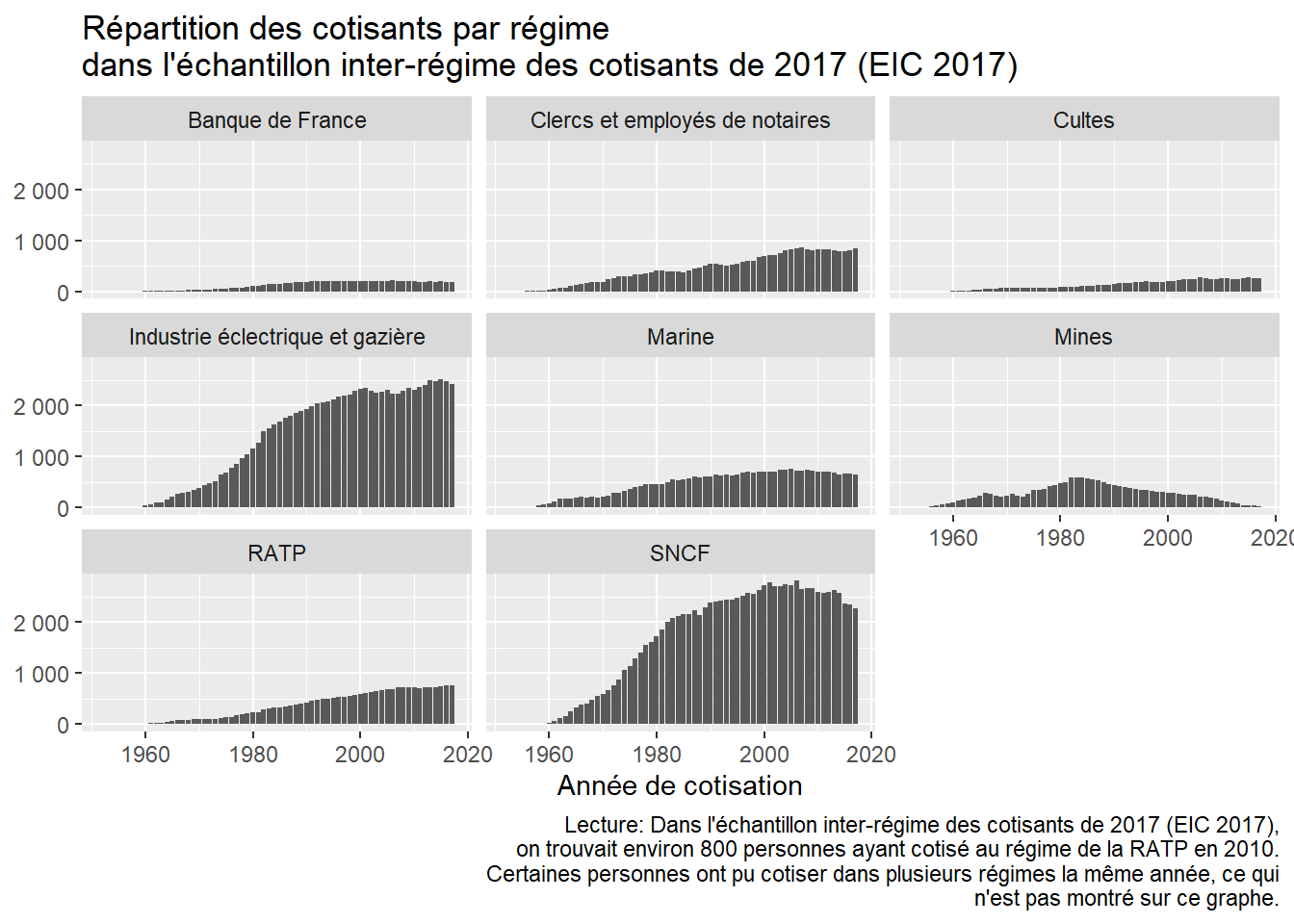
2.19.2 Simplification des régimes complémentaires
De la même façon, Trajectoire retient 8 caisses de complémentaires : l’Arrco, l’Agirc (fusionnée à partir de 2019 avec l’Arrco), l’Ircantec, le RSI complémentaire, la MSA exploitant complémentaire, le Retraite additionnelle de la Fonction publique (Rafp) ainsi que les régimes complémentaire et supplémentaire de la Caisse Autonome de Retraite des Médecins de France (CARMF).
Regroupements des caisses complémentaires
| Caisse initiale (code EIC) | Caisse de référence |
|---|---|
| 1001, 1002 | Ircantec |
| 6000 | Arrco |
| 5000 | Agirc |
| 0041,0043 | RSI complémentaire |
| 3000 | Rafp |
| 0023 | MSA exploitant complémentaire |
| 2014, 2015, 2016, 2022, 2032, 2042, 2052, 2062, 2072, 2082, 2092, 2093, 2102, 2112, 2122, 2212, 2222, 2232 | CARMF complémentaire |
| 2213, 2033, 2043, 2053, 2063, 2073 | CARMF supplémentaire (ASV) |
2.20 Partitionnement de l’EIC en sous-échantillons
Dans Trajectoire, nous ne souhaitons pas créer de champs vides pour des individus, afin que la valeur NA soit spécifiquement réservée aux variables en attente de remplissage (imputation). A partir de l’EIC, nous créons autant de tables que de sous-population d’intérêt et sélectionnons uniquement les variables qui ont un sens pour ces populations. Par exemple, les fonctionnaires sont les seuls pour laquelle la variable “point d’indice” est renseignée. Cette structuration permet également de soulager l’usage de la mémoire vive lors de la simulation, puisque les tables sont chargées sous-population par sous-population.
2.21 Ajout des pondérations individuelles
La documentation de l’EIC annonce que pour inférer des résultats sur population entière, une pondération des individus “sur la base des données démographiques” est nécessaire pour “extrapoler à l’ensemble des individus de 23 à 71 ans au 31 décembre 2017”. La pondération est calculée grâce au Répertoire national d’identification des personnes physiques (RNIPP), par année et trimestre de naissance, le genre et selon si la personne est née ou non en France. Nous corrigeons également les durées inégales d’années et de trimestres.
Avertissement
Dans le RNIPP agrégé par mois, sexe et lieu de naissance (France ou étranger) :
- Certaines personnes nées à l’étranger et immatriculées au RNIPP ne le sont que pour des courts séjours sur le territoire (soins médicaux, études etc.) mais continuent de figurer au répertoire
- Nous ne disposons pas de l’exhaustivité des décès, en particulier pour les périodes les plus anciennes. Il y a donc un surreprésentation de ces populations dans les données.
\[\begin{array}{l} \textrm{ponderation}_i=\frac{\textrm{effectif}\;^{RNIPP}_{gen=gen_i, paysNaissance=paysNaissance_i, sexe=sexe_i} \times \frac{nbJoursTrim_{trim=timNaissance_i}}{nbJoursAnnee_{annee=gen_i}}}{\textrm{effectif}\;^{EIC}_{gen=gen_i, trimNaissance=timNaissance_i, paysNaissance=paysNaissance_i, sexe=sexe_i}} \end{array}\]
Notre correction permet de se rapprocher fortement des effectifs du RNIPP :
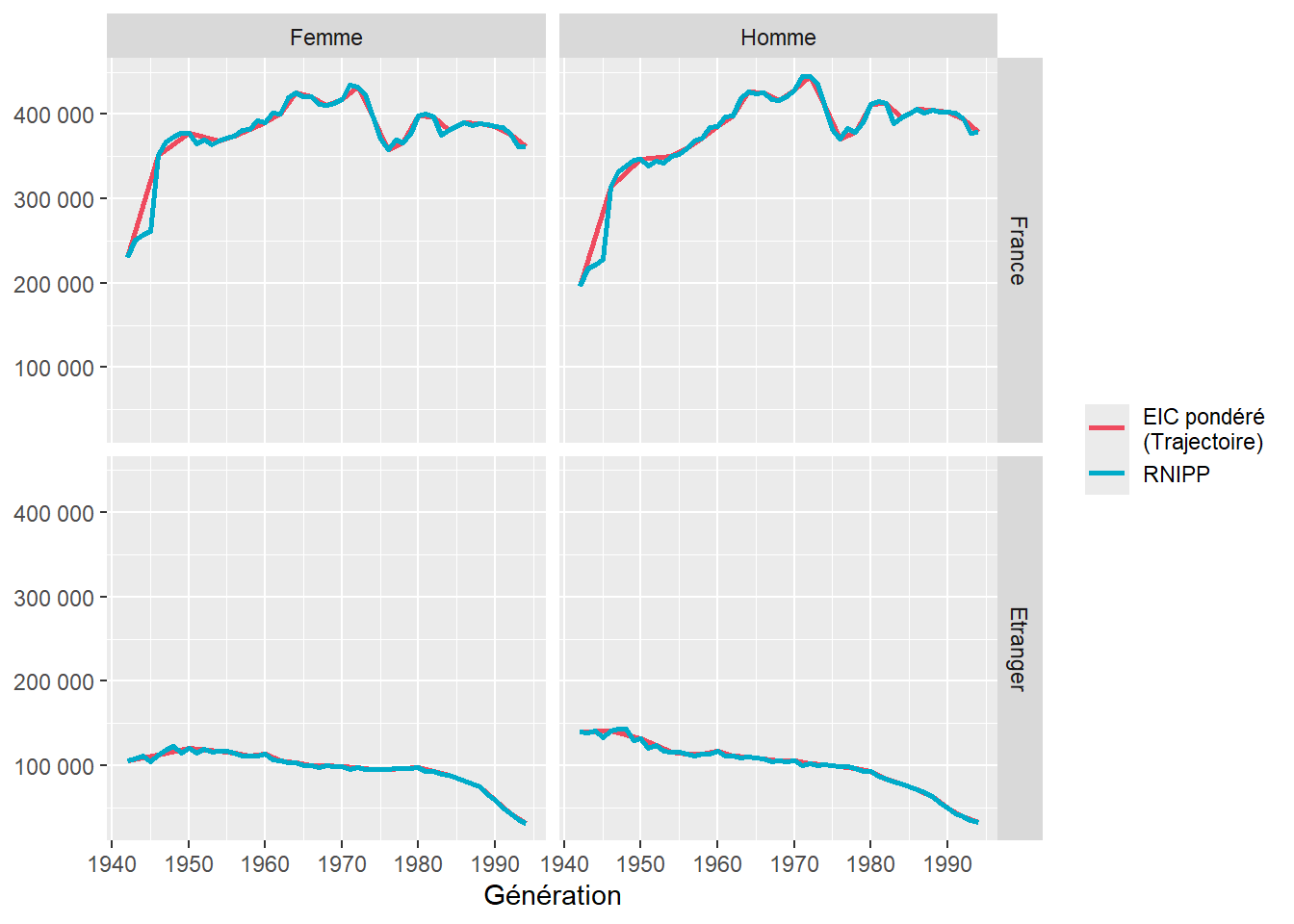
2.22 Tableaux de fréquence par fusion EIC-EIR
L’EIR est l’unique source en notre posession sur plusieurs données : - trimestres validés à l’étranger - timestres de bonification - lieu de résidence pendant la retraite - proportion des “catégories actives” de la fonction publique (voir encadré)
Nous utilisons la dernière génération de l’échantillon à être passée à la retraite; pour laquelle les données sont à la fois les plus complètes et les plus récentes. Pour l’EIC 2017 il s’agit de la génération 1950.
2.23 Dérive de la proportion des “catégories actives” de la fonction publique
Deux corps de la fonction publique avec des effectifs importants, les instituteurs et les infirmières, sont sortis récemment des “catégories actives” (cf. étape 2.22), respectivement à partir de 2011 et 2010. Les générations plus anciennes sont toujours “actives” mais pas les plus récentes, et donc la proportion des “catégories actives” de la fonction publique est amenée à changer significativement.
Trajectoire postule que la proportion de départs en catégorie active sera réduite de moitié d’ici à la génération 1980 du côté du Service de retraites de l’Etat (pour les instituteurs) SRE, et d’ici à la génération 2000 pour la CNRACL (pour les infirmières). Les superactifs ne sont pas touchés.
2.24 Modèle de départ
Pour simuler le passage à la retraite (ou “départ” ou “liquidation des droits”), Trajectoire suppose que chaque personne fait face à un choix chaque trimestre de sa vie : continuer à travailler ou faire valoir ses droits à la retraites. Ce choix est formalisé par un modèle logistique, et pour simplifier on ne considère que les trimestres entre l’âge d’ouverture des droits (AOD) et l’âge d’annulation de la décote (AAD).
Trajectoire postule que le départ dépend essentiellement des caractéristiques suivantes:
la caisse
le genre
la distance au taux plein, prise en compte sous différentes formes :
tpAtteignable, le taux plein du cotisant arrive avant l’AADdistanceTauxPleinNegative, le cotisant n’a pas atteint le taux pleindateTauxPleinExacte, le cotisant est dans son année du taux pleindistanceTPpositiveInverse, 1/(nombre de trimestres après le taux plein), avec l’idée que la plupart des cotisants partent au taux plein, ou juste après, puis de moins en moins
La génération 1950 est retenue pour l’estimation du modèle de départ car c’est la plus récente des générations entièrement partie à la retraite.
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8937 -0.3215 -0.2069 -0.1320 3.0816
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.99901 0.91864 1.087 0.27682
distanceTPpositiveInverse -1.38619 0.53351 -2.598 0.00937 **
dateTauxPleinExacteTRUE -3.62185 1.23213 -2.940 0.00329 **
tpAtteignableTRUE -4.22374 0.63681 -6.633 3.30e-11 ***
trimestreNaissance 0.07729 0.10275 0.752 0.45194
estPolycotisantTRUE -0.83139 0.39256 -2.118 0.03418 *
trimestre2 2.52030 0.47088 5.352 8.69e-08 ***
trimestre3 0.74416 0.53373 1.394 0.16323
trimestre4 0.35331 0.56707 0.623 0.53326
distanceTauxPleinNegativeTRUE -5.21603 0.72213 -7.223 5.08e-13 ***
trimestrePlafondTRUE 0.87931 0.85776 1.025 0.30531
trimestreAodTRUE -13.98699 1010.91586 -0.014 0.98896
dateTauxPleinExacteTRUE:tpAtteignableTRUE 3.46003 1.45106 2.384 0.01710 *
tpAtteignableTRUE:trimestreAodTRUE -0.21994 1220.51838 0.000 0.99986
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 889.79 on 1942 degrees of freedom
Residual deviance: 671.97 on 1929 degrees of freedom
AIC: 699.97
Number of Fisher Scoring iterations: 17
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8118 -0.4794 -0.4246 -0.3715 2.5013
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.00745 0.19655 -15.301 < 2e-16 ***
distanceTPpositiveInverse 0.99915 0.14076 7.098 1.26e-12 ***
dateTauxPleinExacteTRUE -0.04600 0.53566 -0.086 0.93156
tpAtteignableTRUE 0.29863 0.12656 2.360 0.01829 *
trimestreNaissance 0.06613 0.03021 2.189 0.02857 *
estPolycotisantTRUE -0.06520 0.08101 -0.805 0.42092
trimestre2 0.27299 0.12706 2.149 0.03167 *
trimestre3 -0.16309 0.13603 -1.199 0.23057
trimestre4 0.09981 0.13085 0.763 0.44558
distanceTauxPleinNegativeTRUE 0.36451 0.15343 2.376 0.01751 *
trimestrePlafondTRUE 3.81148 0.22180 17.185 < 2e-16 ***
trimestreAodTRUE 1.99690 0.17663 11.306 < 2e-16 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 1.68764 0.57634 2.928 0.00341 **
tpAtteignableTRUE:trimestreAodTRUE -1.36525 0.27540 -4.957 7.15e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 7338.7 on 8245 degrees of freedom
Residual deviance: 6243.9 on 8232 degrees of freedom
AIC: 6271.9
Number of Fisher Scoring iterations: 5
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.9684 -0.1579 -0.1220 -0.1144 3.6483
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.976286 0.072267 -13.509 < 2e-16 ***
distanceTPpositiveInverse 0.684213 0.052463 13.042 < 2e-16 ***
dateTauxPleinExacteTRUE 0.381758 0.101473 3.762 0.000168 ***
tpAtteignableTRUE -1.467804 0.054010 -27.176 < 2e-16 ***
trimestreNaissance 0.033022 0.009322 3.542 0.000396 ***
estPolycotisantTRUE -0.181089 0.024422 -7.415 1.22e-13 ***
trimestre2 0.465297 0.044054 10.562 < 2e-16 ***
trimestre3 -0.061887 0.046179 -1.340 0.180192
trimestre4 -0.052281 0.047123 -1.109 0.267234
distanceTauxPleinNegativeTRUE -3.999845 0.066677 -59.988 < 2e-16 ***
trimestrePlafondTRUE 2.244244 0.085843 26.144 < 2e-16 ***
trimestreAodTRUE 3.433803 0.052146 65.850 < 2e-16 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 2.576509 0.119534 21.555 < 2e-16 ***
tpAtteignableTRUE:trimestreAodTRUE -3.113603 0.075434 -41.276 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 140530 on 197905 degrees of freedom
Residual deviance: 68671 on 197892 degrees of freedom
AIC: 68699
Number of Fisher Scoring iterations: 7
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5159 -0.4638 -0.3185 -0.1492 3.5914
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.61471 0.71118 -0.864 0.387399
distanceTPpositiveInverse 0.07596 0.54504 0.139 0.889157
dateTauxPleinExacteTRUE -1.78505 1.04907 -1.702 0.088839 .
tpAtteignableTRUE -2.44840 0.65644 -3.730 0.000192 ***
trimestreNaissance 0.24688 0.08666 2.849 0.004385 **
estPolycotisantTRUE 0.38769 0.22980 1.687 0.091592 .
trimestre2 -0.29654 0.38495 -0.770 0.441105
trimestre3 -0.64627 0.39755 -1.626 0.104031
trimestre4 -0.23560 0.36688 -0.642 0.520757
distanceTauxPleinNegativeTRUE -4.07540 0.80335 -5.073 3.92e-07 ***
trimestrePlafondTRUE 1.84791 0.67292 2.746 0.006031 **
trimestreAodTRUE 2.51619 0.66749 3.770 0.000164 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 4.31283 1.39548 3.091 0.001998 **
tpAtteignableTRUE:trimestreAodTRUE -2.58828 1.12718 -2.296 0.021662 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1012.74 on 1163 degrees of freedom
Residual deviance: 700.21 on 1150 degrees of freedom
AIC: 728.21
Number of Fisher Scoring iterations: 6
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.9749 -0.1427 -0.1100 -0.0601 3.2868
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.04352 0.78885 -0.055 0.9560
distanceTPpositiveInverse 1.47311 0.70989 2.075 0.0380 *
dateTauxPleinExacteTRUE -2.07735 1.39587 -1.488 0.1367
tpAtteignableTRUE -2.58173 0.58630 -4.403 1.07e-05 ***
trimestreNaissance 0.14646 0.09729 1.505 0.1322
estPolycotisantTRUE 0.58566 0.32562 1.799 0.0721 .
trimestre2 -0.21874 0.48574 -0.450 0.6525
trimestre3 -0.74019 0.51448 -1.439 0.1502
trimestre4 -1.95185 0.80251 -2.432 0.0150 *
distanceTauxPleinNegativeTRUE -4.90633 0.75471 -6.501 7.98e-11 ***
trimestrePlafondTRUE 2.72248 1.31103 2.077 0.0378 *
trimestreAodTRUE 2.32663 0.48882 4.760 1.94e-06 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 17.95651 490.43807 0.037 0.9708
tpAtteignableTRUE:trimestreAodTRUE -15.43480 490.43615 -0.031 0.9749
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1336.92 on 2392 degrees of freedom
Residual deviance: 561.35 on 2379 degrees of freedom
AIC: 589.35
Number of Fisher Scoring iterations: 13
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1876 -0.2134 -0.1589 -0.1439 3.5593
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.25585 0.46134 -0.555 0.57919
distanceTPpositiveInverse 0.59910 0.32083 1.867 0.06186 .
dateTauxPleinExacteTRUE 0.02182 0.58124 0.038 0.97006
tpAtteignableTRUE -1.43154 0.28791 -4.972 6.62e-07 ***
trimestreNaissance 0.05394 0.05551 0.972 0.33124
estPolycotisantTRUE -0.77490 0.27631 -2.804 0.00504 **
trimestre2 0.27742 0.24079 1.152 0.24927
trimestre3 -0.19957 0.25076 -0.796 0.42610
trimestre4 -0.17985 0.25556 -0.704 0.48159
distanceTauxPleinNegativeTRUE -3.55098 0.35213 -10.084 < 2e-16 ***
trimestrePlafondTRUE 2.36930 0.50322 4.708 2.50e-06 ***
trimestreAodTRUE 2.56698 0.27804 9.232 < 2e-16 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 2.90270 0.74337 3.905 9.43e-05 ***
tpAtteignableTRUE:trimestreAodTRUE -2.94006 0.51496 -5.709 1.13e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 3483.1 on 5661 degrees of freedom
Residual deviance: 1994.0 on 5648 degrees of freedom
AIC: 2022
Number of Fisher Scoring iterations: 7
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6289 -0.5327 -0.4558 -0.3993 2.4205
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.353953 0.148983 -15.800 < 2e-16 ***
distanceTPpositiveInverse 0.612677 0.115314 5.313 1.08e-07 ***
dateTauxPleinExacteTRUE -0.397590 0.474972 -0.837 0.40255
tpAtteignableTRUE 0.146561 0.103532 1.416 0.15689
trimestreNaissance 0.005349 0.022800 0.235 0.81451
estPolycotisantTRUE -0.276817 0.050145 -5.520 3.38e-08 ***
trimestre2 -0.014927 0.097364 -0.153 0.87815
trimestre3 -0.128365 0.098227 -1.307 0.19127
trimestre4 0.299321 0.092915 3.221 0.00128 **
distanceTauxPleinNegativeTRUE 0.381561 0.121483 3.141 0.00168 **
trimestrePlafondTRUE 3.157265 0.167512 18.848 < 2e-16 ***
trimestreAodTRUE 1.609727 0.137380 11.717 < 2e-16 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 1.410971 0.496897 2.840 0.00452 **
tpAtteignableTRUE:trimestreAodTRUE -0.623756 0.208719 -2.988 0.00280 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 12203 on 13666 degrees of freedom
Residual deviance: 10810 on 13653 degrees of freedom
AIC: 10838
Number of Fisher Scoring iterations: 5
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1276 -0.3053 -0.2201 -0.1373 4.1145
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.31504 0.46577 2.823 0.00475 **
distanceTPpositiveInverse -1.71932 0.37746 -4.555 5.24e-06 ***
dateTauxPleinExacteTRUE -3.67555 0.59597 -6.167 6.94e-10 ***
tpAtteignableTRUE -4.13539 0.33137 -12.480 < 2e-16 ***
trimestreNaissance 0.06478 0.05537 1.170 0.24202
estPolycotisantTRUE -0.62060 0.18985 -3.269 0.00108 **
trimestre2 1.73805 0.22705 7.655 1.93e-14 ***
trimestre3 0.33052 0.26234 1.260 0.20771
trimestre4 -0.23179 0.29335 -0.790 0.42944
distanceTauxPleinNegativeTRUE -5.61289 0.39738 -14.125 < 2e-16 ***
trimestrePlafondTRUE 0.65750 0.42401 1.551 0.12098
trimestreAodTRUE -0.51293 1.03287 -0.497 0.61947
dateTauxPleinExacteTRUE:tpAtteignableTRUE 4.75819 0.65812 7.230 4.83e-13 ***
tpAtteignableTRUE:trimestreAodTRUE -15.24800 403.04211 -0.038 0.96982
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2675.7 on 6255 degrees of freedom
Residual deviance: 1974.7 on 6242 degrees of freedom
AIC: 2002.7
Number of Fisher Scoring iterations: 17
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6099 -0.4500 -0.4188 -0.3753 2.4655
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.664981 0.235218 -11.330 < 2e-16 ***
distanceTPpositiveInverse 0.814018 0.167688 4.854 1.21e-06 ***
dateTauxPleinExacteTRUE 0.496437 0.508835 0.976 0.3292
tpAtteignableTRUE 0.095173 0.166688 0.571 0.5680
trimestreNaissance 0.009185 0.036678 0.250 0.8023
estPolycotisantTRUE 0.090460 0.111473 0.811 0.4171
trimestre2 0.091023 0.145858 0.624 0.5326
trimestre3 -0.202077 0.151277 -1.336 0.1816
trimestre4 -0.158725 0.151612 -1.047 0.2951
distanceTauxPleinNegativeTRUE -0.132528 0.213214 -0.622 0.5342
trimestrePlafondTRUE 3.378150 0.238182 14.183 < 2e-16 ***
trimestreAodTRUE 1.962842 0.258834 7.583 3.37e-14 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 0.566590 0.604935 0.937 0.3490
tpAtteignableTRUE:trimestreAodTRUE -1.006504 0.411275 -2.447 0.0144 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 5128.5 on 6325 degrees of freedom
Residual deviance: 4445.6 on 6312 degrees of freedom
AIC: 4473.6
Number of Fisher Scoring iterations: 5
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8509 -0.4375 -0.1803 -0.1075 3.4864
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.173407 0.074269 -15.799 < 2e-16 ***
distanceTPpositiveInverse 0.329727 0.052382 6.295 3.08e-10 ***
dateTauxPleinExacteTRUE -0.041808 0.104503 -0.400 0.689107
tpAtteignableTRUE -1.410207 0.057479 -24.534 < 2e-16 ***
trimestreNaissance 0.050692 0.009604 5.278 1.30e-07 ***
estPolycotisantTRUE -0.080059 0.022608 -3.541 0.000398 ***
trimestre2 0.566611 0.043141 13.134 < 2e-16 ***
trimestre3 0.115875 0.044903 2.581 0.009863 **
trimestre4 0.089381 0.045774 1.953 0.050862 .
distanceTauxPleinNegativeTRUE -3.256051 0.067199 -48.454 < 2e-16 ***
trimestrePlafondTRUE 2.178844 0.081134 26.855 < 2e-16 ***
trimestreAodTRUE 2.674340 0.063997 41.789 < 2e-16 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 3.370088 0.115920 29.072 < 2e-16 ***
tpAtteignableTRUE:trimestreAodTRUE -2.880534 0.075398 -38.205 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 100911 on 127014 degrees of freedom
Residual deviance: 60238 on 127001 degrees of freedom
AIC: 60266
Number of Fisher Scoring iterations: 7
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.2129 -0.5065 -0.4785 -0.2705 2.6750
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.76152 0.59123 -2.979 0.00289 **
distanceTPpositiveInverse 0.10717 0.27001 0.397 0.69143
dateTauxPleinExacteTRUE 0.38465 0.92587 0.415 0.67781
tpAtteignableTRUE -0.41308 0.54334 -0.760 0.44709
trimestreNaissance 0.12586 0.05485 2.295 0.02174 *
estPolycotisantTRUE -0.06753 0.12425 -0.544 0.58678
trimestre2 -0.37845 0.20432 -1.852 0.06399 .
trimestre3 -0.37102 0.19616 -1.891 0.05857 .
trimestre4 -0.38627 0.20074 -1.924 0.05433 .
distanceTauxPleinNegativeTRUE -1.65352 0.49516 -3.339 0.00084 ***
trimestrePlafondTRUE 0.95654 0.42412 2.255 0.02411 *
trimestreAodTRUE 2.26483 0.57653 3.928 8.55e-05 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 0.57315 0.98479 0.582 0.56057
tpAtteignableTRUE:trimestreAodTRUE -1.58775 0.73719 -2.154 0.03126 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2499.7 on 2840 degrees of freedom
Residual deviance: 2167.8 on 2827 degrees of freedom
AIC: 2195.8
Number of Fisher Scoring iterations: 6
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8947 -0.2124 -0.1723 -0.1594 3.5763
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.03999 0.46748 -2.225 0.02610 *
distanceTPpositiveInverse 0.85574 0.41498 2.062 0.03920 *
dateTauxPleinExacteTRUE -1.75682 0.59175 -2.969 0.00299 **
tpAtteignableTRUE -1.95870 0.35924 -5.452 4.97e-08 ***
trimestreNaissance 0.03733 0.06844 0.545 0.58550
estPolycotisantTRUE 0.57902 0.24566 2.357 0.01842 *
trimestre2 0.08382 0.28663 0.292 0.76995
trimestre3 -0.07277 0.28446 -0.256 0.79810
trimestre4 -0.19377 0.29651 -0.653 0.51344
distanceTauxPleinNegativeTRUE -3.27532 0.42993 -7.618 2.57e-14 ***
trimestrePlafondTRUE 3.84087 0.47881 8.022 1.04e-15 ***
trimestreAodTRUE 1.23506 0.44049 2.804 0.00505 **
dateTauxPleinExacteTRUE:tpAtteignableTRUE 4.51044 0.69493 6.490 8.56e-11 ***
tpAtteignableTRUE:trimestreAodTRUE -1.19635 0.55259 -2.165 0.03039 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2263.9 on 4271 degrees of freedom
Residual deviance: 1325.9 on 4258 degrees of freedom
AIC: 1353.9
Number of Fisher Scoring iterations: 7
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6175 -0.5133 -0.2262 -0.1626 3.4603
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.17722 0.27826 -4.231 2.33e-05 ***
distanceTPpositiveInverse 0.44231 0.17848 2.478 0.01320 *
dateTauxPleinExacteTRUE 0.59799 0.44173 1.354 0.17582
tpAtteignableTRUE -1.25984 0.20312 -6.203 5.55e-10 ***
trimestreNaissance 0.03396 0.03425 0.992 0.32144
estPolycotisantTRUE 0.37109 0.13717 2.705 0.00682 **
trimestre2 0.23608 0.14157 1.668 0.09540 .
trimestre3 -0.07524 0.14472 -0.520 0.60314
trimestre4 -0.29547 0.15449 -1.913 0.05581 .
distanceTauxPleinNegativeTRUE -2.98252 0.23525 -12.678 < 2e-16 ***
trimestrePlafondTRUE 1.06534 0.37564 2.836 0.00457 **
trimestreAodTRUE 2.05589 0.20709 9.928 < 2e-16 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 2.08851 0.48540 4.303 1.69e-05 ***
tpAtteignableTRUE:trimestreAodTRUE -2.68864 0.27660 -9.720 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 6842.8 on 9170 degrees of freedom
Residual deviance: 4820.3 on 9157 degrees of freedom
AIC: 4848.3
Number of Fisher Scoring iterations: 6
Call:
stats::glm(formula = liquidationPrecise ~ distanceTPpositiveInverse +
dateTauxPleinExacte * tpAtteignable + trimestreNaissance +
estPolycotisant + trimestre + distanceTauxPleinNegative +
trimestrePlafond + trimestreAod * tpAtteignable, family = stats::binomial(logit),
data = dtIdTrimEir2, na.action = stats::na.exclude, model = FALSE,
x = FALSE, y = FALSE)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5992 -0.4590 -0.4185 -0.3567 2.4570
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.11387 0.15844 -13.342 < 2e-16 ***
distanceTPpositiveInverse 0.20197 0.14315 1.411 0.15825
dateTauxPleinExacteTRUE 0.54634 0.32557 1.678 0.09333 .
tpAtteignableTRUE -0.17735 0.10999 -1.612 0.10688
trimestreNaissance 0.02641 0.02664 0.991 0.32145
estPolycotisantTRUE -0.11328 0.05760 -1.967 0.04922 *
trimestre2 -0.26232 0.10144 -2.586 0.00971 **
trimestre3 -0.54871 0.10826 -5.068 4.01e-07 ***
trimestre4 0.02813 0.09622 0.292 0.77003
distanceTauxPleinNegativeTRUE -0.04157 0.13207 -0.315 0.75294
trimestrePlafondTRUE 2.94049 0.16433 17.893 < 2e-16 ***
trimestreAodTRUE 1.58682 0.14473 10.964 < 2e-16 ***
dateTauxPleinExacteTRUE:tpAtteignableTRUE 0.02213 0.36329 0.061 0.95142
tpAtteignableTRUE:trimestreAodTRUE -0.53872 0.22551 -2.389 0.01690 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 9616.0 on 12562 degrees of freedom
Residual deviance: 8538.9 on 12549 degrees of freedom
AIC: 8566.9
Number of Fisher Scoring iterations: 5
Limites. Trajectoire prend correctement en compte des variations marginales et indépendantes des paramètres principaux (AOD, AAD, DAR), mais pas par exemple un déplacement simultané de ces trois paramètres ! En effet, l’âge lui-même n’est pas pris en compte comme moteur de départ, puisque l’estimation est faite sur une seule génération. La variable trimestreNaissance, qui sur une génération peut être interprétée comme l’âge en trimestres, n’est significative que pour les liquidations à la CNAV.
Par ailleurs, ce modèle de départ ne s’adapte pas à un régime à point.
2.25 Mortalité différentielle selon le niveau de pension
La forte différence d’espérance de vie entre les plus riches et les pauvres des cotisants impacte fortement le bilan du système de retraites, et il est donc impératif d’affiner les estimations de mortalité par tranches de revenu / patrimoine. Dans Trajectoire, ce sont les pensions qui s’approchent le plus du niveau de vie. Ainsi, pour chaque génération entre les EIR 2012 et 2016, Trajectoire calcule les probabilités de décès par quartile de pension. Trajectoire s’assure par ailleurs que la mortalité de chaque génération reste conforme aux prédictions de l’INSEE par calage sur marge.
Ces coefficients de mortalité sont utilisés pour imputer un âge de décès à chaque individu à l’étape 4.1.
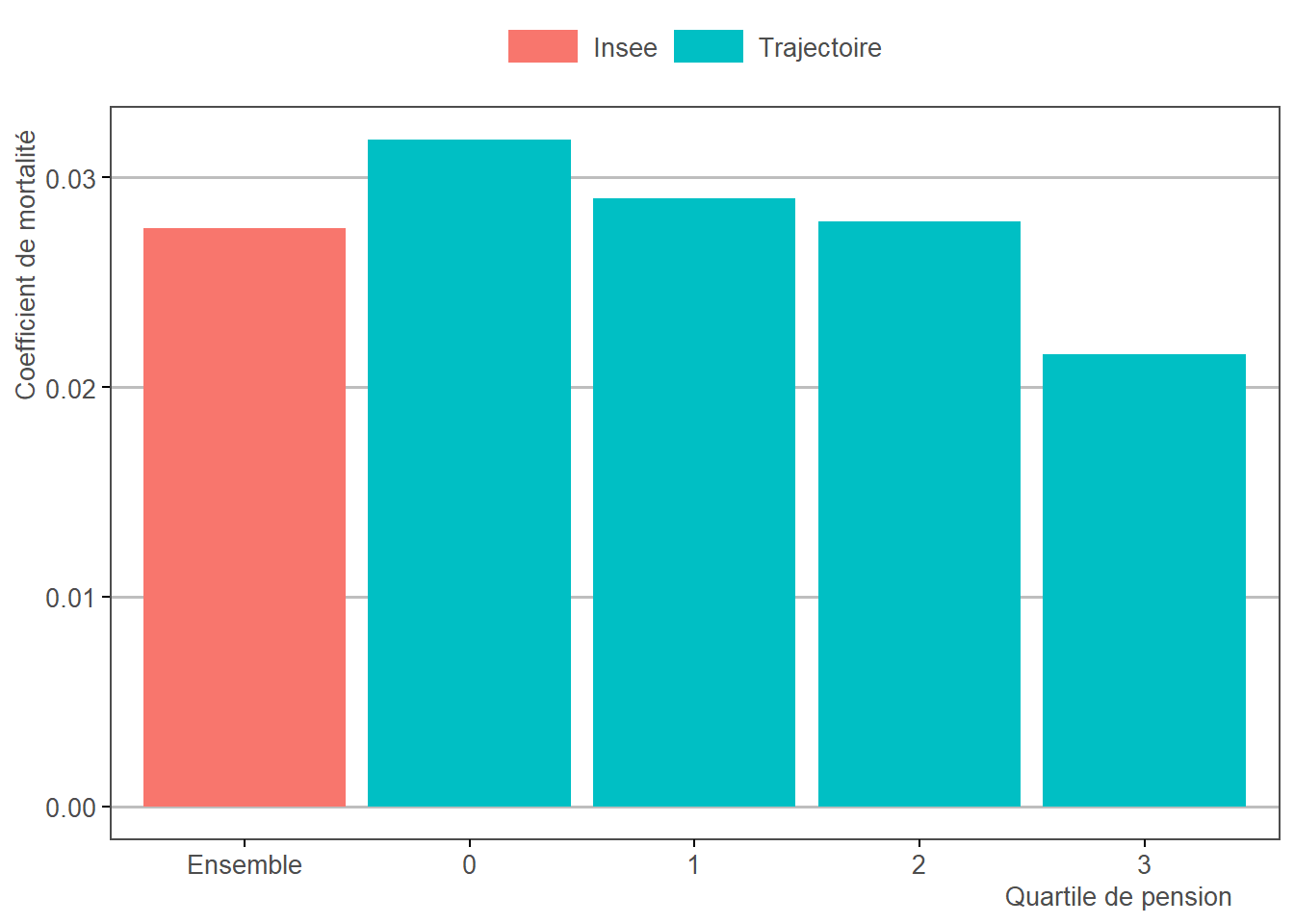
Limites. La mortalité différentielle est estimée en excluant donc les individus décédés avant 2012 et cela engendre probablement une sur-représentation des individus les plus riches (qui ont davantage survécu jusque-là). De plus, la mortalité différentielle est estimée via les EIR 2012 et 2016 et cette fenêtre de 4 années est limitée pour une bonne estimation des différences de mortalité.
2.26 Modélisation du non-recours aux pensions
Certaines personnes n’exercent pas (la totalité de) leur droit à la pension. Il s’agit en général de personne ayant travaillé en France pendant de courtes durées (non recours total), ou de polypensionnés ayant oublié de faire valoir leurs droits dans une autre caisse que celle liée à leur activité principale (non-recours partiel). Ces situations baissent tendentiellement avec l’informatisation des traitements. Voir “Non-recours : à 70 ans, un tiers des assurés n’ont pas fait valoir tous leurs droits à retraite” (2019) pour plus d’information.
Trajectoire estime le non-recours en prenant comme référence les individus de la génération 1946 vivants dans le dernier EIR disponible. Il suffit de comparer les pensions qu’ils ont effectivement liquidées avec celles auxquelles ils auraient pu prétendre d’après les données de l’EIC : la différence constitue le non-recours. Le non-recours est utilisé à la étape 7.3.
Non-recours total. Les hommes, les étrangers et les personnes ayant cotisé peu ont tendance à moins faire valoir leurs droits à la retraite. L’effet du nombre de caisse est contre-intuitif: avoir cotisé dans plusieurs caisses diminue le non recours, car on a plus de chance de faire valoir ses droits dans au moins une caisse.
Non-recours partiel. Pour les poly-cotisants qui ont liquidé au moins un caisse, une équation de non-recours partiel est estimée, régime par régime. Le non-recours dépend principalement de la durée cotisée dans ce régime : plus une personne a cotisé longtemps, moins elle “oublie” de faire valoir ses droits.
2.27 Modélisation de l’inaptitude
Certaines personnes sont reconnues inaptes au travail à l’approche de l’âge de la retraite. Trajectoire modélise une telle liquidation des droits pour inaptitude à l’aide d’un modèle de survie (ou modèle de durée), sur la génération 1950 (génération commune à l’EIC et l’EIR). Ce modèle permet d’immaginer un âge d’inaptitude pour les nouvelles générations, ce qui est fait à la étape 4.23.
Les variables explicatives utilisées sont le sexe et le nombre de trimestres cotisés entre 50 et 55 ans (variable categ: de 0 à 10 trimestres en référence, puis de 10 à 20 trimestres et plus de 20 trimestres). Les hommes “survivent” moins longtemps i.e. sont déclarés inaptes plus vite ; les personnes ayant beaucoup cotisé entre 50 et 55 ans “survivent” plus longtemps i.e. sont moins souvent déclarées inaptes.
2.28 Distribution de la quotité de travail des fonctionnaires
Le fait pour un fonctionnaire de travailler à temps partiel impacte de deux façons distinctes ses droits à la retraite. Le nombre de trimestre comptant pour l’ouverture des droits, ou durée validée, est indépendante de la quotité, alors que celui comptant pour le calcul de la propratisation, ou “durée de services, ne tient compte que du temps de travail effectif et dépend donc de si le fonctionnaire est à temps partiel ou non.
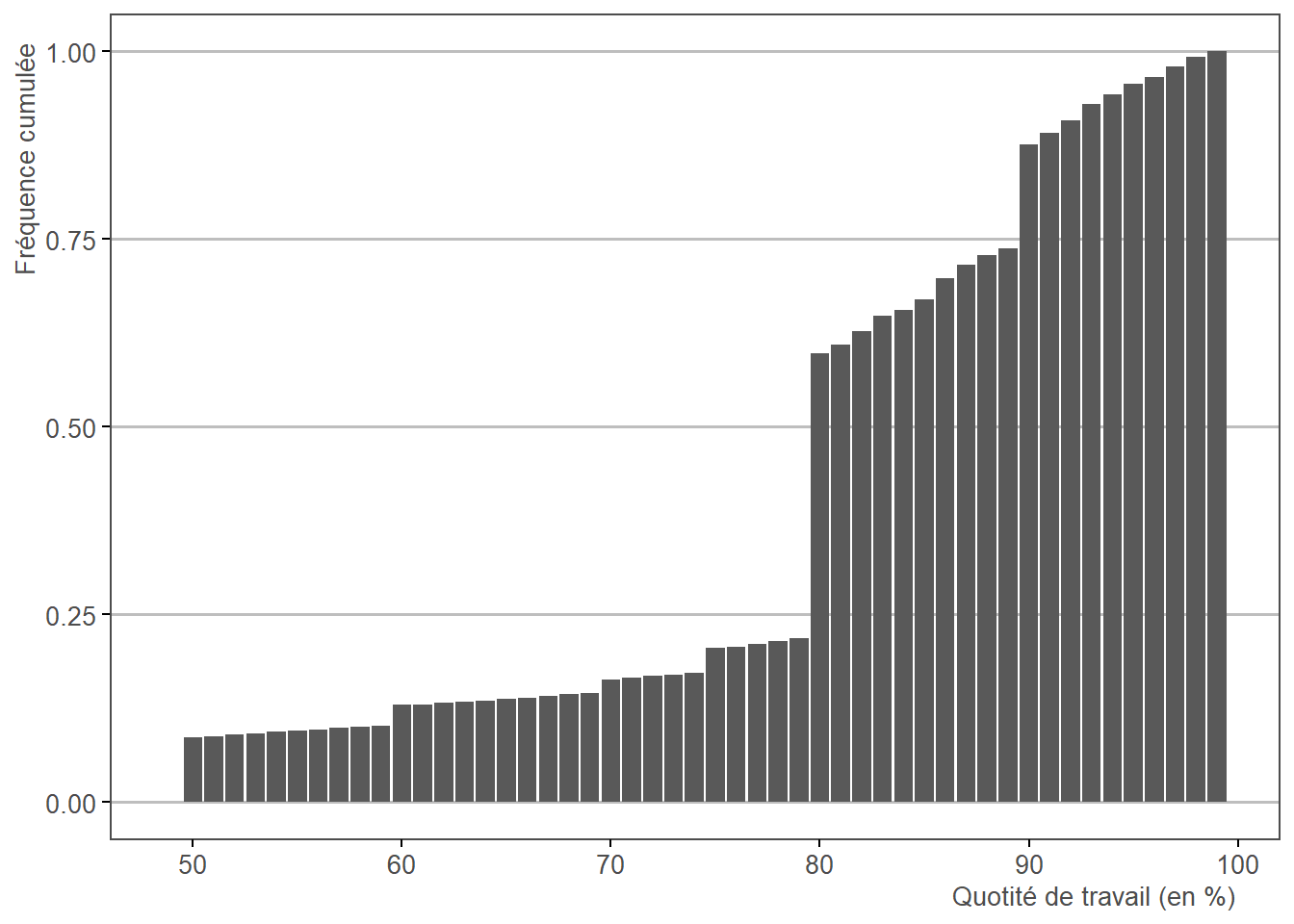
Trajectoire détermine cette quotité chaque année pour chaque cotisant dans chaque régime où il cotise (à savoir le SRE pour la fonction publique d’Etat et le CNARCL pour la fonction publique territoriale et hosptialière (CNARCL), en divisant la durée de services par la durée validée. Une personne ayant changé de quotité de travail en cours d’année aura une quotité constatée intermédiaire, ce qui explique la distribution des quotités dans le graphique suivant.
Cette quotité de travail est utilisée ultérieurement à la étape 3.6, étape 3.31 et étape 3.30.
2.29 Choix de la méthode de prolongement des séries temporelles
Trajectoire associe à chaque série temporelle passée une série et une méthode de prolongement pour les années non observées (variables serieReference et typeSerieReference). Le mois d’évolution est aussi spécifié (1 pour janvier, 12 pour décembre).
2.30 Echantillonage (optionnel)
Dans un souci de réduire le temps d’exécution du modèle (notamment lors de phases de développement du modèle), il est possible d’échantillonner les données utilisées par Trajectoire. Ce tirage est stratifié par année et mois de naissance, sexe et selon si la personne est née en France ou à l’étranger. Nous estimons que les résultats commencent à se stabiliser au-dessus d’un taux d’échantillonnage de 10%.